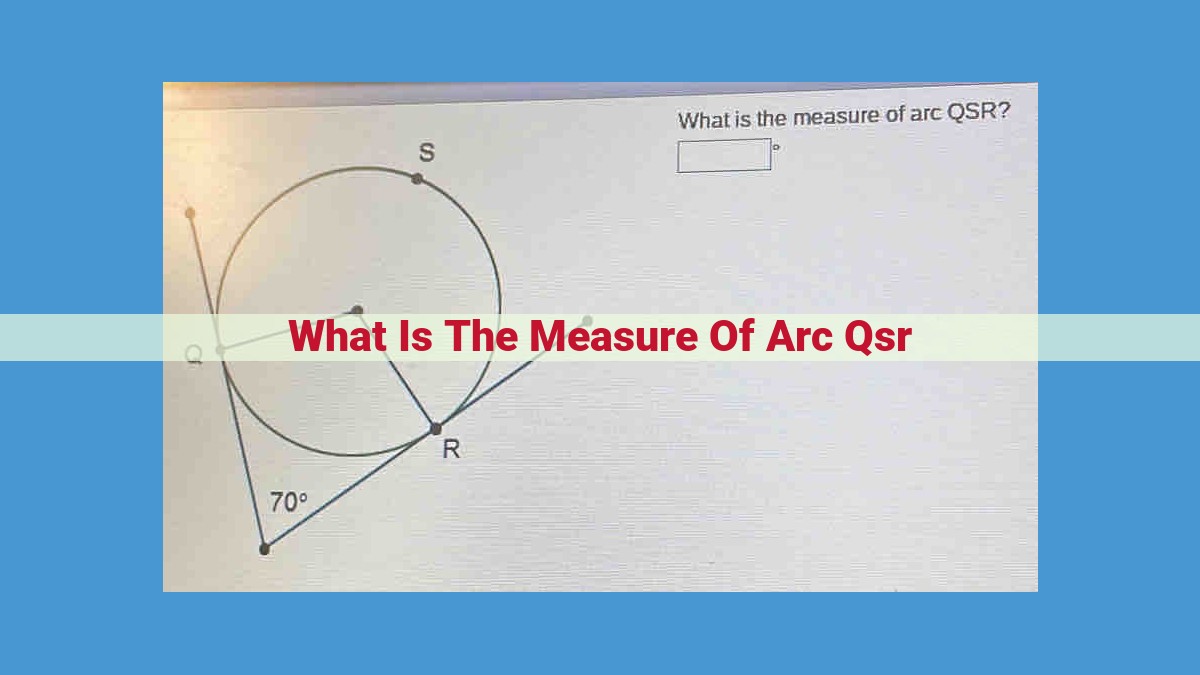
The measure of arc QSR is determined by the corresponding central angle ∠QSR and the radius of the circle. The relationship between arc length, central angle, and radius is given by the formula Arc Length = Radius * Central Angle (in radians). To find the measure of arc QSR, convert the central angle ∠QSR from degrees to radians and multiply it by the radius of the circle. The result will give you the length of arc QSR.
Exploring the Arcs and Angles of a Circle
Ladies and gentlemen, prepare to embark on a journey into the enchanting realm of geometry, where the mysteries of arc length, central angles, and radii await our exploration. Today, we delve into the first chapter of this adventure: understanding arc length.
Unveiling Arc Length
In the world of circles, arc length refers to the distance along the curved edge. Just like a devious villain plotting a cunning heist, arc length seeks to unravel the secrets of a circle’s circumference. And just as a skilled detective needs the perfect formula to crack a case, we have the arc length formula at our disposal:
Arc Length = Radius × Central Angle (in radians)
The Symphony of Arc Length, Circumference, and Radians
The arc length formula reveals an enchanting dance between three elements: arc length, circumference, and radians. The circumference represents the total distance around a circle, while radians measure central angles in terms of the circle’s radius.
Imagine a circle with a circumference of 10π units. If we have an arc that spans an angle of 2π radians (a full circle), then its arc length would also be 10π units. This beautiful harmony showcases the integral relationship between these three concepts.
Examples of Arc Length Calculations
To illuminate the practical application of our arc length knowledge, let’s dive into a few examples. Suppose we have a circle with a radius of 5 units and a central angle of 60 degrees. To determine its arc length, we convert degrees to radians first:
60 degrees × (π/180 degrees) ≈ 1.047 radians
Plugging this into the arc length formula, we get:
Arc Length = 5 units × 1.047 radians ≈ 5.236 units
So, our arc would stretch across 5.236 units along the circle’s edge. By mastering arc length calculations, we gain a deeper understanding of the intricacies of circular geometry.
Exploring Central Angles
- Definition and properties of central angles
- Conversion between degrees and radians
- Relationship between central angles and sectors
Exploring Central Angles: Unlocking the Secrets of Circle Geometry
In the realm of geometry, circles hold a special place, their harmonious curves and intricate measurements captivating scholars for centuries. Among their key elements are central angles, pivotal concepts that provide a gateway to understanding the hidden beauty of circles.
Central Angles Defined
A central angle is an angle formed by two radii of a circle. These radii emanate from the circle’s center, creating two distinct regions. The vertex of the central angle lies at the circle’s center, while its two arms extend outward. Central angles measure the fraction of the circle’s circumference that they intercept.
Properties of Central Angles
Central angles possess several remarkable properties:
- Arc Length: The length of the intercepted arc is directly proportional to the measure of the central angle. In other words, larger central angles enclose larger arcs.
- Area of Sector: The area of the sector formed by a central angle is also proportional to the angle’s measure. This means that sectors with larger central angles occupy a greater portion of the circle’s area.
- Inscribed Angle: An inscribed angle, or an angle formed by two chords intersecting inside a circle, is always half the measure of the central angle that intercepts the same arc. This relationship is known as the Inscribed Angle Theorem.
Conversion Between Degrees and Radians
Central angles can be measured in either degrees or radians. Degrees are the familiar unit we encounter in daily life, while radians represent the ratio of the intercepted arc length to the circle’s radius. The conversion between degrees and radians is given by:
1 radian = 180 degrees / π
This conversion is crucial for many geometric calculations involving circles, as radians often simplify expressions and equations.
Relationship Between Central Angles and Sectors
A sector is a region of a circle bounded by two radii and the intercepted arc. The area of a sector is given by the following formula:
Area of Sector = (1/2)r²θ
where r is the radius of the circle and θ is the measure of the central angle in radians. This formula underscores the direct proportionality between the central angle and the sector’s area.
The Role of Radius: Understanding the Essence of Circles
In the realm of geometry, the radius stands as a pivotal concept that unravels the secrets of circles. It serves as the lifeline that connects the center to any point on the circle’s circumference, defining its size and shaping its properties.
Definition and Properties of a Radius
A radius is a line segment that originates from the center of a circle and terminates on its circumference. It represents the constant distance from the center to every point on the circle’s edge. Interestingly, all radii of a given circle are congruent, meaning they have the same length.
Relationship Between Radius, Diameter, and Circumference
The radius plays a crucial role in determining the diameter and circumference of a circle. The diameter, which is the distance across the circle through the center, is twice the length of the radius. Moreover, the circumference, which is the distance around the circle, is 2π times the radius. These relationships provide essential insights into the proportions and dimensions of circles.
Significance of Radius in Area and Volume Calculations
The radius is also a fundamental parameter in calculating the area and volume of circles and spheres. The area of a circle can be determined by the formula πr², where r represents the radius. Similarly, the volume of a sphere, which is a three-dimensional shape, can be calculated using the formula 4/3πr³, again highlighting the significance of the radius in defining the size and capacity of these geometric objects.
Understanding the role of the radius empowers us with a comprehensive understanding not only of circles but also of related concepts like spheres and cylinders. It allows us to analyze, compare, and solve problems involving circular shapes with greater accuracy and ease.