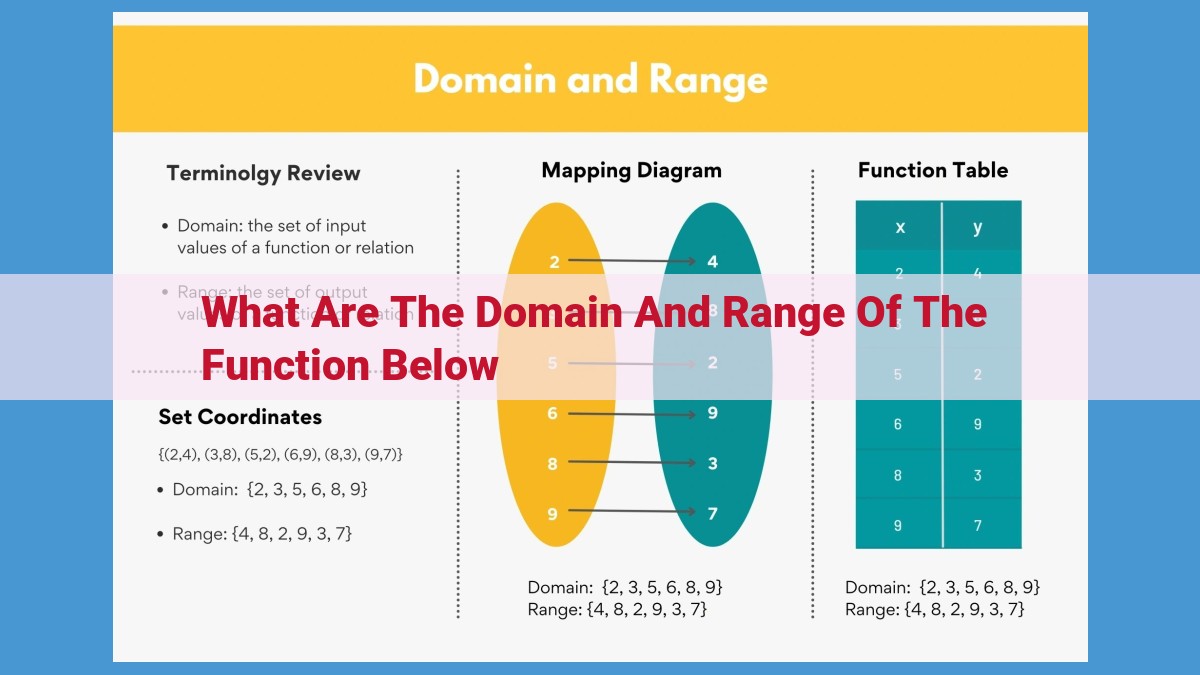
The domain and range of a function define the input and output values, respectively. The domain is the set of possible input values, while the range is the set of possible output values. Understanding the domain and range is crucial for analyzing functions, determining their behavior, and applying them in various contexts. By defining the domain and range, we establish the boundaries of the function and ensure its well-definedness.
- Definition and importance of the domain and range of a function.
Understanding the Domain and Range of a Function: The Gates to a Mathematical World
Imagine you’re a chef creating a delicious dish. Before you start cooking, you need to know what ingredients you’ll use and what you’re aiming to make. In the world of mathematics, functions behave similarly. They take input values (ingredients) and produce output values (the dish). The domain defines the set of possible inputs, while the range defines the set of possible outputs.
The Domain: The Chef’s Pantry
The domain of a function is like the chef’s pantry, containing all the ingredients they can use. It represents the set of all possible input values that the function can handle. The domain is often described using mathematical symbols, such as the variable x, which represents the independent variable (the input).
The Range: The Culinary Masterpiece
The range of a function is analogous to the finished dish, the result of the chef’s culinary artistry. It defines the set of all possible output values that the function can produce. Just as a chef carefully selects ingredients to create a specific flavor profile, a function’s range is determined by the relationship between the input and output.
The Interplay: A Dance of Inputs and Outputs
The domain and range of a function are interconnected. The input values (domain) influence the output values (range). For instance, if a chef uses a certain amount of salt, it will directly impact the dish’s saltiness. Understanding this relationship is crucial for analyzing and manipulating functions.
Determining the Domain and Range: Unlocking the Culinary Secrets
Determining the domain and range of a function is like unraveling a culinary recipe. There are various methods to do this:
- Analyze the function’s definition: Examine the mathematical expression of the function to identify any restrictions or limitations on the input values.
- Graph the function: Plot the input and output values on a graph to visualize the domain and range.
- Use algebraic techniques: Employ mathematical operations and rules to find the boundaries of the domain and range.
Comprehending the domain and range of functions is a cornerstone of mathematical understanding. It provides insights into the behavior and limitations of functions. Moreover, this knowledge finds practical applications in fields such as engineering, science, and data analysis, where functions are used to model real-world phenomena.
Unlock the Secrets of Functions: Embrace the Domain and Range
Just as a chef masters the art of selecting ingredients and crafting exquisite dishes, understanding the domain and range of a mathematical function is essential for proficient mathematical exploration. Embrace this knowledge, and you’ll become a culinary master of the mathematical realm.
The Domain of a Function: Where the Function’s Story Begins
In the world of functions, the domain is like the character who sets the story in motion. It’s the set of all possible input values that can be plugged into the function to produce an output. Think of it as the range of choices you have when you’re picking a number or variable to start with.
The domain is closely linked to the independent variable, often represented as x. It’s the variable you control or choose, like selecting the starting point of a journey. The domain tells you the range of starting points, or input values, that are allowed for the function to work its magic.
Consider the function f(x) = x + 2. The domain of this function is all numbers, both positive and negative, because any number can be plugged into x and will result in a valid output. In this case, the domain is the set of all real numbers.
Understanding the domain is essential for defining a well-behaved function. It sets the boundaries for the input values and ensures that the function produces meaningful outputs. Without a well-defined domain, the function would be like a boat without a rudder, floating aimlessly without direction.
Range: A Function’s Output Symphony
In the realm of functions, the range unveils the enchanting world of possible outputs that spring from the input values. Think of it as a musical score composed by the function itself. Like the harmonious notes that fill an orchestra, the range encompasses all the melodies that the function can produce.
Unveiling the Secret of the Dependent Variable
Unlocking the mystery of range requires us to delve into the captivating realm of the dependent variable. This variable dances to the tune of the input values, assuming different guises as the function weaves its magic. The range is the captivating stage where these transformations take place, showcasing the full spectrum of values that the dependent variable can embody.
Calculating the Range: A Journey of Discovery
To uncover the secrets of a function’s range, we embark on a mathematical expedition. Through meticulous analysis, we can identify the highest and lowest values that the function can reach. Alternatively, a graphical representation of the function can paint a vivid picture, revealing the range as the vertical span of its curve.
The Interplay of Domain and Range: A Dynamic Duet
Like two dancers in a graceful waltz, domain and range engage in an intricate interplay. The domain dictates the permissible input values, while the range unveils the corresponding output values. Together, they craft a story of interdependency, each element shaping the other’s existence.
The Interrelation between Domain and Range: A Vital Connection in Functions
Functions are like recipes in mathematics that take input values, or domain, and convert them into output values, or range. Just like you can’t make a cake without ingredients, a function can’t produce output without input.
The domain is the set of all possible input values that make the function work properly. It’s like the ingredients of your cake recipe; you can’t substitute coffee for flour, or else the cake will be a disaster.
Similarly, the range is the set of all possible output values that the function generates. It’s like the types of cakes you can make with the recipe; you can make a chocolate cake, a vanilla cake, or a red velvet cake, but you can’t make a pizza.
Understanding the domain and range of a function is crucial because it helps us define its boundaries. Without a specified domain, the function could produce nonsensical output values for inputs that it wasn’t designed to handle. Likewise, without a specified range, we wouldn’t know what kind of output to expect from the function.
Therefore, when defining a function, it’s essential to specify both its domain and range to ensure that it’s well-defined and provides meaningful results.
Unveiling the Enigma of Domain and Range: Methods for their Discovery
In the realm of mathematics, functions are like magic wands, transforming input values into enigmatic outputs. To fully unravel the mystery behind these transformations, it’s imperative to comprehend two fundamental concepts: the domain and the range.
Unveiling the Domain
The domain represents the kingdom of permissible input values that the function can conjure. To ascertain this domain, scrutinize the function’s structure. Spot any restrictions or limitations that dictate which values are admissible as inputs. For instance, if a function involves a division by x, it’s forbidden for x to dance with the forbidden number zero.
Revealing the Range
The range, on the other hand, unveils the spectrum of possible output values that the function can produce. This enchanting set can be gleaned by analyzing the function’s behavior. Trace the output values as the input values traverse their domain, mapping out the boundaries of the function’s output realm.
Graphical Insight
Sometimes, a visual aid can illuminate the domain and range with crystal clarity. Plot the function on a graph, and the domain will emerge as the horizontal span of the curve, while the range will gracefully unfold as the vertical reach.
Decoding Function Definitions
The function definition itself can hold clues to its domain and range. If the function is defined by an equation, examine the constraints or conditions imposed on the input variable. These boundaries often delineate the domain. As for the range, it can sometimes be deduced from the nature of the function itself—for instance, a quadratic function’s range always lies above a certain point.
Examples Illuminate
To solidify our understanding, let’s embark on a practical adventure. Consider the function f(x) = x + 2. Analyzing the structure reveals no restrictions on x, so its domain is the entire set of real numbers. Tracing the output values unveils that the function’s output can roam freely across the real number line, revealing its range as the entire set of real numbers as well.
The Domain and Range of a Function: Unveiling the Boundaries of Functions
In the realm of mathematics, functions play a crucial role in modeling and analyzing relationships between input and output values. Understanding a function’s domain and range unlocks the key to comprehending its behavior and limitations. Let’s embark on an exploration of these fundamental concepts.
Domain: The Realm of Input Values
The domain of a function represents the set of all permissible input values. It defines the acceptable values that the independent variable can assume. The independent variable is often denoted by x and represents the input of the function. Whether it’s a range of numbers, a specific set of values, or an interval, the domain establishes the boundaries within which the function can operate.
Range: The Spectrum of Output Values
In contrast to the domain, the range of a function encompasses the set of all possible output values. It determines the variety of values that the dependent variable can take on. The dependent variable is typically denoted by y and represents the output of the function. By analyzing the range, we gain insights into the outcomes produced by the function for different inputs.
Interplay of Domain and Range
The relationship between the domain and range is akin to a dance between input and output values. The domain restricts the acceptable inputs, while the range defines the corresponding outputs. This interplay ensures that the function operates within well-defined boundaries, connecting the input values with their respective outputs.
Example: Unraveling the Domain and Range of f(x) = x + 2
Let’s delve into a concrete illustration of determining the domain and range of a function. Consider the function f(x) = x + 2. The independent variable x can assume any real number, as there are no restrictions or limitations imposed on its values. Therefore, the domain of f(x) is all real numbers, denoted as (−∞, ∞).
Now, let’s examine the range of f(x). For any value of x, the output y = x + 2 can be any real number. This is because the addition of a constant (2) to any real number results in another real number. Hence, the range of f(x) is also all real numbers, or (−∞, ∞).
Significance and Applications
Grasping the concepts of domain and range is paramount for comprehending functions. They provide a framework for understanding the input-output behavior, enabling us to analyze functions, graph them, and solve equations. In real-world applications, identifying the domain and range is essential for ensuring the validity and accuracy of models and calculations.