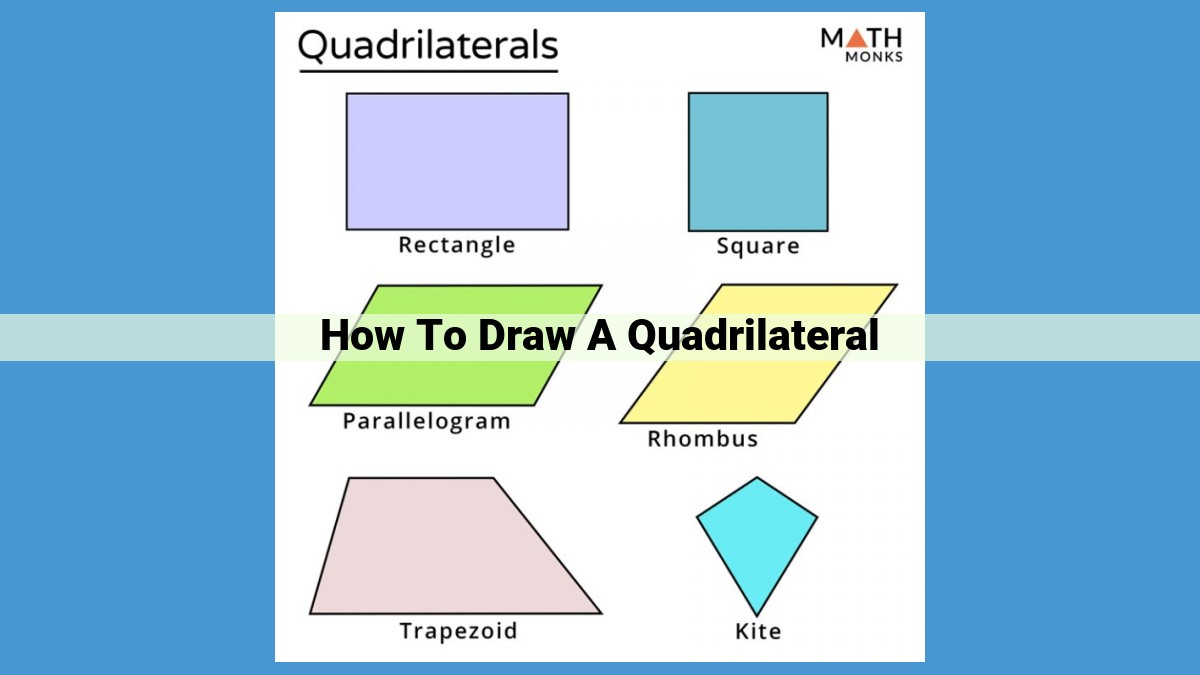
How to Draw a Quadrilateral
To draw a quadrilateral, start by defining the polygon and related terms. Then, follow these steps:
- Draw a line segment to form one side.
- From the endpoint, draw another line segment parallel to the first to form an adjacent side.
- Continue drawing parallel line segments to complete the remaining two sides.
- Join the endpoints of the final side to close the shape.
Unlocking the Secrets of Quadrilaterals: A Comprehensive Guide for Beginners
Embark on a fascinating journey into the realm of geometry, where we unravel the enigmatic world of quadrilaterals. Dive deep into their intriguing characteristics, unravel their hidden secrets, and gain a profound understanding of these captivating shapes.
Unveiling Quadrilaterals: The Guardians of Four Sides
To begin our quest, we must define the very essence of a quadrilateral. It is a captivating polygon, a geometrical figure composed of four sides and four vertices, forming a closed loop. Each side is a line segment that connects two of the four vertices.
Exploring the Vocabulary of Quadrilaterals: A Lexicon of Shapes
In the world of quadrilaterals, we encounter a symphony of shapes, each with its unique charm:
- Parallelogram: A quadrilateral where opposite sides are parallel.
- Rectangle: A parallelogram with four right angles.
- Square: A rectangle with all sides equal.
- Trapezoid: A quadrilateral with exactly one pair of parallel sides.
- Kite: A quadrilateral with two pairs of adjacent sides equal.
Unveiling the Hidden Properties of Quadrilaterals: A Symphony of Relationships
Quadrilaterals possess a harmonious interplay of properties that define their very nature. The opposite sides of a quadrilateral are equal in length, and the diagonals, line segments connecting opposite vertices, bisect the opposite angles. This delicate balance creates a geometric tapestry of symmetry and harmony.
**Dive into the Art of Drawing Quadrilaterals: A Step-by-Step Guide**
Let’s embark on an engaging journey into the world of quadrilaterals. These geometric shapes with four sides and four vertices play a fundamental role in various fields, from architecture to engineering. To fully comprehend these fascinating shapes, let’s dive into the art of drawing them.
Step 1: Begin with a Blank Canvas
Start with a piece of paper and a pencil. Imagine a blank canvas where you’ll create your quadrilateral masterpiece.
Step 2: Establish the Endpoints
Determine the starting point and the ending point of your first side. Mark these points clearly as they will form the foundation of your quadrilateral.
Step 3: Connect the Dots
Using a ruler or straight edge, connect the two endpoints to form the first side. Ensure that the line is straight and the length matches your desired shape.
Step 4: Repeat for Remaining Sides
Repeat steps 2 and 3 to create the remaining three sides of your quadrilateral. Each side should connect two vertices and follow the desired length and angle measurements.
Step 5: Close the Shape
The final step is to connect the last endpoint to the starting point, forming the fourth and final side. Ensure that all sides align seamlessly to create a closed shape.
Congratulations! You have now successfully drawn a quadrilateral, the building block of many complex and intriguing geometric shapes.
Types of Quadrilaterals
In the realm of geometry, quadrilaterals reign supreme as polygons with four sides and vertices. These fascinating shapes come in various forms, each with its own distinctive characteristics.
Parallelogram
Think of a parallelogram as a quadrilateral where opposite sides are parallel and congruent. Its parallel sides give it an air of balance and symmetry. Whether it’s a flat piece of paper or the design of a quilt, parallelograms bring a touch of order to the world.
Rectangle
A rectangle is a special parallelogram that takes it up a notch. Not only are its opposite sides parallel, but all four sides are equal in length. Picture a perfectly square football field or a crisp, rectangular piece of toast.
Square
The square is the epitome of quadrilateral perfection. It’s a rectangle with all four sides equal and all four angles measuring a neat 90 degrees. Think of the dice you roll in a board game or the iconic shape of a Rubik’s Cube.
Trapezoid
A trapezoid is a quadrilateral with a little asymmetry. It has one pair of parallel sides and the other two sides sloping towards each other like a trapezoidal kite soaring through the sky.
Kite
A kite is a quadrilateral with a unique twist. Two of its adjacent sides are equal in length and the other two are also equal in length. Picture the shape of a diamond ring or the wings of a majestic eagle.
Understanding these different types of quadrilaterals is like having a secret code to unlock the world of shapes. They appear in countless places, from the architecture of buildings to the patterns in nature. Embrace the beauty and diversity of quadrilaterals, and let them inspire your creativity.
Properties of Quadrilaterals: A Journey into Symmetry and Geometry
As we delve deeper into the fascinating world of quadrilaterals, let’s explore some of their intriguing properties that reveal the underlying harmony of these geometric shapes.
The Opposites Attract: Relationship Between Opposite Sides and Diagonals
In a quadrilateral, the opposite sides are the two pairs of sides that lie directly across from each other. Interestingly, these opposite sides share a special connection. In certain types of quadrilaterals, such as parallelograms and rectangles, opposite sides are equal in length and parallel to each other. This symmetry creates a sense of balance and regularity.
Diagonals: Bisecting Opposite Angles
Diagonals are line segments that connect opposite vertices of a quadrilateral. These diagonals play a crucial role in determining the shape’s properties. One remarkable property is that diagonals bisect, or cut into two equal parts, the opposite angles of the quadrilateral. This phenomenon adds to the quadrilateral’s structural stability and symmetry.
Measuring Quadrilaterals: A Journey into Precision
When it comes to understanding quadrilaterals, measuring their sides and angles is crucial for comprehensive analysis. Join us on a storytelling adventure as we delve into the fascinating world of quadrilateral measurement, equipping you with the tools to master this essential aspect of geometric exploration.
Measuring the Sides: A Ruler’s Precision
Imagine yourself as an architect designing a beautiful building. To ensure the structural integrity of your masterpiece, you need to accurately measure the lengths of each side of the quadrilateral walls. This is where a humble ruler comes into play. Place its edge along the side of the quadrilateral, starting from one vertex and aligning it with the edge. Mark the endpoint on the ruler, and you’ve got the measurement of the side.
Unveiling the Angles: A Protractor’s Guidance
Now, let’s turn our attention to measuring the angles between the sides. Picture yourself as an artist capturing the beauty of a geometric landscape. To accurately portray the angles of the quadrilateral, you’ll need a protractor. Center the protractor at the vertex where two sides meet, aligning the baseline with one side. Mark the intersection of the second side with the protractor’s scale to determine the angle measure.
Practical Applications: Beyond the Classroom
The knowledge of measuring quadrilaterals extends far beyond the confines of the classroom. In the bustling world of architecture, quadrilaterals form the foundation of structures, from towering skyscrapers to quaint cottages. Precise measurements ensure the stability and aesthetic appeal of these architectural marvels. Similarly, in engineering, quadrilaterals play a vital role in designing bridges, vehicles, and countless other creations where accuracy is paramount.
Angle Sum of Quadrilaterals
- Prove the angle sum theorem for quadrilaterals.
- Emphasize the significance of 360 degrees for interior angles.
Angle Sum of Quadrilaterals
Prove the Angle Sum Theorem for Quadrilaterals
Embark on a mathematical journey to uncover the angle sum theorem for quadrilaterals. Just like any room in your house has four corners, a quadrilateral is a shape with four straight sides and four corner points, or vertices. Imagine a rectangular room where the walls meet at each corner, forming right angles.
Now, let’s walk around this room, starting at one corner and measuring the angles at each vertex. You’ll be amazed to find that the sum of these angles always equals 360 degrees. This fascinating observation is known as the angle sum theorem for quadrilaterals.
Significance of 360 Degrees for Interior Angles
Why is 360 degrees so special? It represents the complete turn of a circle. As you walk around the room, you’re essentially making a full turn. The fact that the sum of the interior angles of any quadrilateral equals 360 degrees tells us that all four walls of the room fit together perfectly, forming a complete enclosure.
Applications in Architecture, Design, and Engineering
Understanding the angle sum theorem for quadrilaterals is not just a theoretical exercise. It has practical applications in architecture, design, and engineering. For example, architects use this theorem to ensure that the angles of a building’s walls add up to 360 degrees, ensuring structural stability. It also helps engineers calculate the angles of beams and bridges to ensure their strength and durability.
The angle sum theorem for quadrilaterals is a fundamental concept in geometry with far-reaching implications. Whether you’re designing a room, building a structure, or simply curious about the world around you, understanding this theorem will open up new possibilities for exploration and comprehension.
Diagonals of Quadrilaterals: Unraveling Their Significance and Mathematical Charm
In the realm of quadrilaterals, diagonals play a pivotal role, connecting opposite vertices and unveiling hidden geometric relationships. This article delves into the fascinating world of diagonals, exploring their properties, intriguing intersections, and practical applications.
Connecting Opposite Vertices
Diagonals are straight lines that connect opposite vertices within a quadrilateral. These lines cut through the quadrilateral, forming two triangles that share the same base.
Intersecting at a Special Point
One of the most remarkable properties of diagonals is that they intersect at a single point, known as the intersection point. This point divides both diagonals into equal segments. If you imagine the quadrilateral folded in half along a diagonal, the intersection point becomes the point where the folded edges touch.
Calculating Diagonals
The lengths of diagonals can be calculated using various formulas. For parallelograms, the diagonals are perpendicular bisectors of each other, meaning they cut each other at right angles and divide each other into equal segments. The length of a diagonal in a parallelogram can be found using the formula:
Diagonal Length = √(Side 1² + Side 2²)
Applications in Real-World Scenarios
Quadrilaterals and their diagonals find myriad applications in engineering, architecture, and design. For example, in bridge construction, the diagonals provide structural support by forming triangular trusses that distribute weight evenly. In architecture, diagonals can be used to create dynamic and visually appealing building facades.
Diagonals are not just lines that cut through quadrilaterals; they are geometric treasures that hold hidden relationships and practical significance. By understanding their properties and applications, we unlock a deeper appreciation for the fascinating world of geometry and its relevance in shaping our built environment.
Applications of Quadrilaterals: From Blueprint to Canvas
Embrace the Versatility of Geometric Shapes
Quadrilaterals, with their four sides and four vertices, play a pivotal role not only in the realm of mathematics but also in diverse fields of human endeavor. These geometric shapes find practical applications in architecture, design, and engineering, shaping our physical environment and enriching our digital world.
Architectural Marvels: A Symphony of Quadrilaterals
In the realm of architecture, quadrilaterals serve as the building blocks of iconic structures. Consider the soaring skyscrapers, their faces adorned with geometric patterns of rectangles and parallelograms. These shapes provide stability and support, allowing buildings to reach new heights and redefine urban skylines.
Bridges: Triumphs of Engineering and Geometrical Ingenuity
Quadrilaterals also play a vital role in engineering feats, particularly in the design of bridges. Suspension bridges, with their graceful curves, are essentially composed of quadrilaterals that distribute weight and create a sturdy framework. These structures embody the harmony between mathematics and engineering, connecting communities and inspiring awe.
Computer Graphics: Painting with Pixels and Polygons
Even in the digital realm, quadrilaterals find their place. In computer graphics, quadrilaterals form the fundamental units of many 3D models. From the curved surfaces of landscapes to the sharp edges of buildings, quadrilaterals provide the geometric infrastructure for virtual worlds. They allow artists and designers to create immersive experiences that push the boundaries of imagination.
Everyday Encounters: Quadrilaterals in Disguise
But the applications of quadrilaterals extend beyond grand structures and virtual landscapes. In our everyday lives, we encounter quadrilaterals in countless forms. The pages of our books, the screens of our devices, and even the shapes of our buildings all feature quadrilaterals. These geometric shapes serve as the unseen backbone of our physical and digital environments, enhancing their functionality and aesthetics.
Quadrilaterals, from the humble rectangle to the intricate trapezium, embody the versatility of geometric shapes. Their applications span across disciplines, from architecture to engineering to computer science, shaping the world around us and fueling our technological advancements. As we continue to explore the world of mathematics, let us appreciate the profound impact of quadrilaterals, the building blocks of our physical and digital realities.