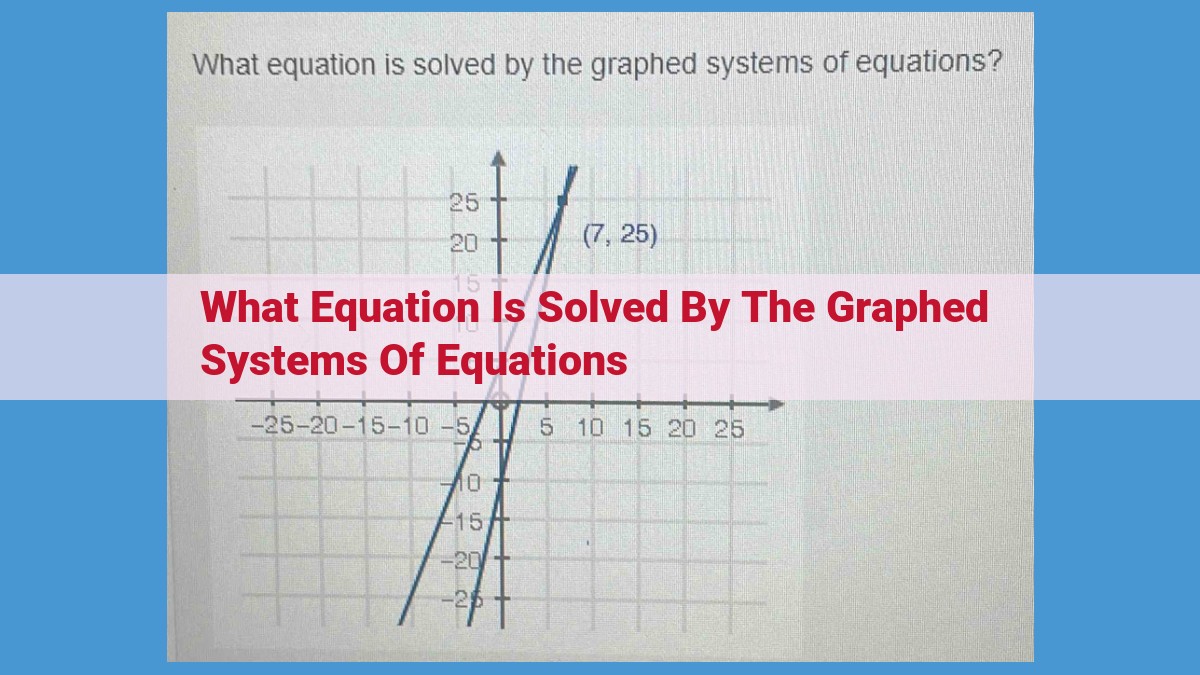
The graphed systems of equations solve for the values of unknown variables that satisfy both equations simultaneously. Intersecting lines represent systems with one solution, while parallel lines indicate no solution and coincident lines show infinitely many solutions. By analyzing the intersection point (for intersecting lines) or the relative positions (for parallel and coincident lines), we can graphically determine the solution or absence of solution to the systems of equations.
Systems of Equations: Unveiling the Power of Graphical Representations
Step into the captivating world of systems of equations, where the interplay of variables and equations paints a vivid picture of mathematical relationships. A system of equations is a set of two or more equations that share common variables. Visualizing these relationships through graphical representations empowers us to uncover their solutions with remarkable clarity.
Graphical Representation: A Journey from Equations to Lines
Just as words convey ideas, equations capture mathematical concepts. However, sometimes, a visual depiction can illuminate these concepts even more vividly. When it comes to systems of equations, the graphical representation takes center stage. Each equation is transformed into a line on a coordinate plane, with its slope and y-intercept dictating its path.
The dance of these lines on the graph forms a mesmerizing tapestry, revealing the heart of the system of equations. The points where these lines intersect, if any, represent the solutions to the system. These solutions are the values of the variables that simultaneously satisfy both equations in the system.
Unveiling the Story behind the Graphs
This graphical representation is not merely a visual aid; it’s a powerful storytelling tool. Let’s delve into the captivating narratives that different line configurations reveal:
Intersecting Lines: The Tale of Two Solutions
When two lines intersect, their meeting point whispers the secrets of two distinct solutions. These solutions represent the values of the variables that make both equations true. Pictorially, the intersection point is the stage where the lines share a common dance.
Parallel Lines: A Journey with No Destination
Ah, parallel lines—the enigmatic dancers that never meet. Their paths run side by side, eternally separated. This graceful parallelism signifies that the system of equations has no solution. The lines are like ships passing in the night, destined to remain forever apart.
Coincident Lines: A Harmonic Duet
Coincident lines are the harmonious twins of the graphical world. They overlap perfectly, forming a single line that sings the same tune. This graphical representation indicates that the system of equations has infinitely many solutions. The lines are inseparable, like two sides of the same coin.
In the realm of systems of equations, graphical representations serve as invaluable compasses, guiding us towards their secrets. They illuminate the relationships between equations, reveal solutions, and unveil the nature of the system. By capturing the interplay of variables on a coordinate plane, these graphs breathe life into mathematical concepts, transforming equations into a mesmerizing dance of lines.
Intersecting Lines
- Define intersecting lines and describe their characteristics.
- Discuss how the graph of intersecting lines illustrates the solution.
- Show the connection between intersecting lines and solving equation systems.
Intersecting Lines: Unraveling the Essence of Systems of Equations Visually
When you encounter a system of equations, think of it as two straight lines inhabiting the same two-dimensional plane. These lines can either intersect, forming a single point of intersection, or they can remain parallel, never crossing paths.
Intersecting Lines: A Crossroads of Solutions
Intersecting lines are characterized by their distinct slopes and y-intercepts. When they meet, they create a unique point of intersection, the solution to the system of equations. Graphically, this point represents the coordinates where the two lines cross.
Solution Unveiled: Reading the Graph
The graph of intersecting lines provides a visual depiction of the solution. The point of intersection indicates the values of the variables that simultaneously satisfy both equations. By locating this point, you can determine the unique solution to the system.
Connection to Equation Systems: A Graphical Interpretation
The graphical representation of intersecting lines establishes a direct link between the system of equations and its solution. If the lines intersect, there is a single solution to the system. This is because the point of intersection represents the values that make both equations true simultaneously.
Example: Unlocking the Secret
Consider the system of equations:
2x + 5y = 11
x - y = 3
Graphing these equations reveals two intersecting lines that cross at the point (2, 1). This point is the solution to the system, as it satisfies both equations concurrently.
Parallel Lines: No Solution in Sight
In the realm of systems of equations, we encounter various scenarios, including the intriguing case of parallel lines. These lines run side by side, never crossing paths, leaving us with a significant conclusion: no solution.
Defining Parallel Lines
Parallel lines are lines that maintain a constant distance from each other. They never intersect, stretching out indefinitely without converging. Their slopes are equal, and their y-intercepts may differ.
Graphical Representation of Parallel Lines
When we graph two equations that represent parallel lines, we observe two distinct lines running side by side. These lines do not touch at any point, signifying the absence of a solution.
No Solution: Why It Happens
The reason for the no solution scenario lies in the equations themselves. For parallel lines, the equations have the same slope but different y-intercepts. This means that the lines will never cross, as they are parallel and have different vertical positions.
Solving Systems with Parallel Lines
When attempting to solve a system of equations involving parallel lines, the result is always the same: no solution. The equations are inconsistent, meaning they do not have a common solution that satisfies both equations.
Coincident Lines: The Enigma of Infinite Solutions
In the realm of systems of equations, where lines dance and intersect, we encounter a fascinating entity known as coincident lines. These peculiar lines, while distinct in their existence, possess an intriguing property that sets them apart.
Coincident Lines: A Definition
Coincident lines are lines that lie exactly upon one another, perfectly superimposed, such that they occupy the same geometric space. In essence, they are two identical lines occupying the same position.
Graphical Representation: A Canvas of Infinite Solutions
When graphed, coincident lines appear as a single line, as if drawn with a double stroke. This visual representation hints at their hidden secret: an infinite number of solutions.
Each point along the single line represents a solution to the system of equations. Why so? Because every point on a coincident line satisfies both equations simultaneously. Imagine a tightrope walker effortlessly balancing on a single strand, effortlessly navigating the delicate equilibrium.
Connection to Solving Equation Systems
The existence of coincident lines has a profound impact on solving systems of equations. When solving a system, we seek pairs of values that satisfy both equations. With coincident lines, every point along the line qualifies as a solution. This infinite set of solutions presents itself metaphorically as a vast ocean of possibilities.
In essence, coincident lines obliterate the notion of a single solution. Instead, they unveil a tapestry of infinite solutions, echoing the boundless wonders of the universe itself.
Coincident lines, with their enigmatic nature and infinite solutions, serve as a reminder of the multifaceted tapestry of mathematics. By understanding this unique line configuration, we unlock the power of visualizing and solving complex equation systems. And in the realm of knowledge, every revelation weaves the fabric of our intellectual tapestry, expanding our comprehension of the world around us.