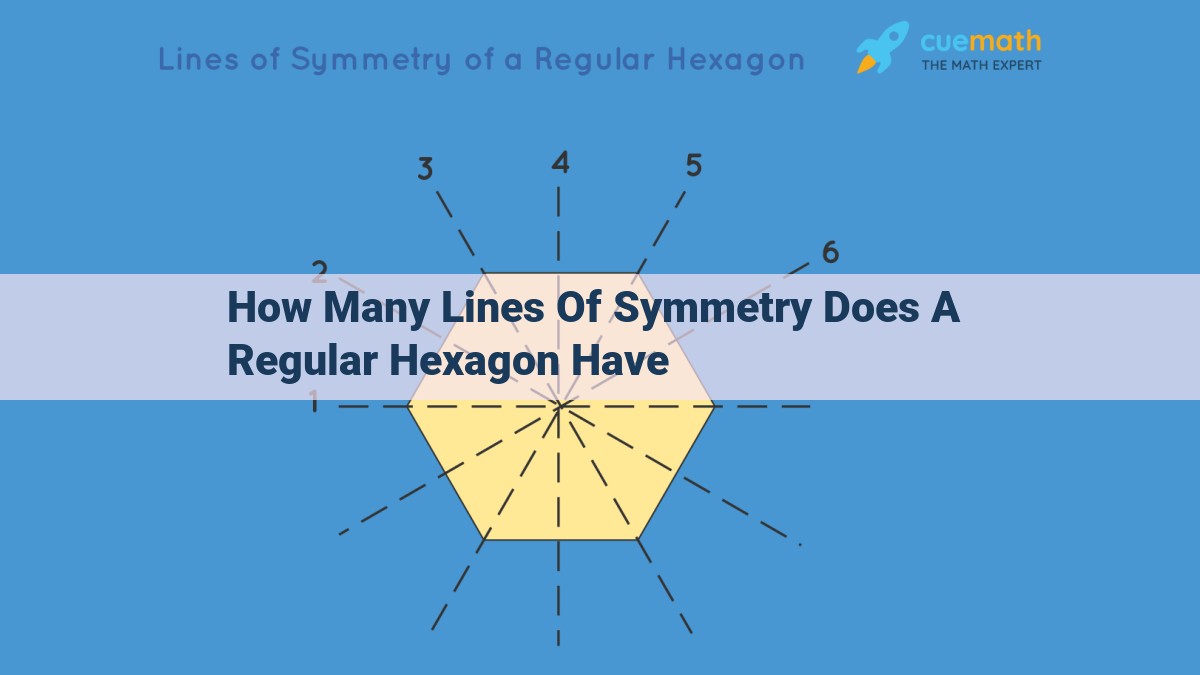
A regular hexagon, known for its symmetry, possesses a remarkable 6 lines of symmetry. This intricate characteristic stems from the figure’s rotational symmetry of order 6. Each of these lines divides the hexagon into two congruent parts, mirroring its shape and size. The regular hexagon’s equilateral (equal sides) and equiangular (equal angles) nature further contributes to its high degree of symmetry, making it an intriguing example of geometrical harmony.
Symmetry in Geometry: Unveiling the Hidden Harmony in Shapes
Imagine a world without symmetry, where objects lacked balance and order. Our eyes would dart aimlessly across chaotic forms, unable to find solace in the harmonious interplay of shapes. Fortunately, we live in a world brimming with symmetry, a fundamental concept that governs the beauty and structure of countless geometrical wonders.
Defining Line of Symmetry
At the heart of symmetry lies the line of symmetry, an imaginary line that divides a shape into two congruent halves. This line is like a mirror, reflecting one side of the shape onto the other. In geometry, the presence of a line of symmetry plays a crucial role, ensuring the equal distribution of points, angles, and sides.
The Regular Hexagon: A Symphony of Sides and Angles
Among the fascinating shapes in the realm of geometry, the regular hexagon stands out as a beacon of symmetry. With its six equal sides and six equal angles, this polygon embodies perfection. Its equilateral nature means its sides are of the same length, and its equiangular character grants it angles of equal measure.
Symmetry in the Regular Hexagon
The regular hexagon is not only defined by its sides and angles but also by its exceptional symmetry. It possesses an astonishing six lines of symmetry, a testament to its rotational symmetry of order 6. These lines of symmetry are the result of the hexagon’s ability to be rotated by 60-degree increments while maintaining its original shape.
The Significance of Symmetry in Geometry**
Symmetry is not merely an aesthetic concept; it has profound implications in geometry. It simplifies the analysis of shapes, as it allows us to study only half of a symmetrical figure, knowing that the other half mirrors it. Symmetry also affects the properties of regular polygons, such as the number of diagonals, area, and perimeter.
The Interplay of Transformations in Symmetry**
The concept of symmetry is inextricably linked to three fundamental transformations: reflection, rotation, and translation. Reflection flips a shape over a line of symmetry, mirroring its points. Rotation turns a shape around a fixed point, maintaining its shape and size. Translation slides a shape from one position to another without altering its orientation or dimensions.
Symmetry is an essential concept that permeates the world of geometry, bringing balance and order to countless shapes and figures. From the simple line of symmetry to the intricate patterns of regular hexagons, symmetry reveals the hidden harmony that underpins the structural beauty of our surroundings. By understanding the principles of symmetry, we gain a deeper appreciation for the aesthetics and mathematical elegance that make geometry such a fascinating field.
Regular Hexagons: Unveiling Their Geometric Symmetry
In the realm of geometry, shapes hold secrets that reveal their hidden patterns and symmetries. Among these enigmatic figures, the regular hexagon stands out as a beacon of symmetry and structural harmony. Delve into the captivating world of regular hexagons as we explore the mesmerizing connection between their properties and the fundamental principles of symmetry.
A Hexagon’s Defining Traits
A regular hexagon is a polygon with six equal sides and six equal angles. This unique combination of sides and angles lends it a distinct equilateral and equiangular nature. The sides are all congruent, ensuring that the hexagon has a uniform shape. Similarly, the angles are all congruent, creating a precise and balanced structure. This harmonious arrangement of sides and angles is what sets a regular hexagon apart from other polygons.
Understanding Symmetry in Geometry
Symmetry plays a pivotal role in geometry, offering insights into the order and balance within shapes. Symmetry generally refers to the existence of identical parts on opposite sides of a central axis or point. In the context of regular polygons, symmetry is often associated with three fundamental transformations: reflection, rotation, and translation.
Rotational Symmetry in Regular Hexagons
Regular hexagons possess remarkable rotational symmetry. The term “rotational symmetry” describes a shape’s ability to be rotated around its center by a specific number of degrees and still maintain its original appearance. In the case of a regular hexagon, it has six lines of symmetry. This means that it can be rotated 60 degrees six times before returning to its original orientation. This rotational symmetry is a fundamental property of regular hexagons and gives them their distinct shape and visual appeal.
Line of Symmetry in Regular Hexagons: Unveiling the Secrets of Geometric Symmetry
Delve into the fascinating world of geometry and discover the captivating concept of symmetry that lies at the heart of many shapes. From the intricate patterns of a snowflake to the harmonious architecture of a cathedral, symmetry has played a pivotal role in shaping the aesthetic beauty and structural integrity of our surroundings.
Symmetry: A Geometrical Dance
Symmetry is a fundamental property of geometric shapes that describes the existence of balance and order. When a shape can be folded, rotated, or translated to create an identical image, it is said to possess symmetry.
Reflection symmetry occurs when a shape can be folded along a line to create two perfectly matching halves. Rotation symmetry involves rotating a shape around a fixed point to achieve the same result. Translation symmetry refers to the movement of a shape along a straight line without changing its orientation.
Regular Hexagons: A Showcase of Symmetry
Regular hexagons, with their six equal sides and angles, are a prime example of shapes that exhibit remarkable symmetry. These polygons are equilateral, meaning they have equal side lengths, and equiangular, meaning they have equal angle measures.
6 Lines of Symmetry: A Rotational Symmetry Story
Regular hexagons showcase a special type of symmetry known as rotational symmetry. This means that the hexagon can be rotated around its center by 60 degrees six times to create identical images.
This rotational symmetry of order 6 gives rise to six lines of symmetry. Each line of symmetry passes through a vertex and the midpoint of the opposite side, dividing the hexagon into two congruent halves.
Symmetry in Geometry: A Guiding Principle
Symmetry is not just an aesthetic consideration; it also plays a significant role in the properties of geometric shapes. Regular polygons, such as hexagons, exhibit higher levels of symmetry which translate into greater stability and structural integrity.
- Regular polygons: Equal sides and angles give regular polygons their distinct appearance and predictable properties. Symmetry enhances these properties, making regular polygons useful in a variety of applications, from architecture to engineering.
Symmetry in Geometry: Unlocking the Order and Beauty of Shapes
Symmetry is a fundamental concept in geometry that captivates our eyes and minds with its intricate order and harmony. Its presence in the world around us, from the patterns on a butterfly’s wings to the structure of a snowflake, reveals the underlying beauty and organization of nature. In this article, we delve into the fascinating world of symmetry in geometry, exploring its significance and revealing how it shapes the properties of regular polygons, including the remarkable regular hexagon.
Understanding Symmetry
Symmetry, in its essence, is the balanced distribution of elements around a central point, line, or plane. It’s like a mirror image that creates a sense of equilibrium and order. In geometry, symmetry manifests in three primary transformations: reflection, rotation, and translation.
- Reflection: Imagine folding a paper along a line, creating a perfect mirror image on both sides. This is reflection symmetry.
- Rotation: Picture a figure rotating around a fixed point, like a child on a merry-go-round. If, after a complete turn, the figure looks the same, it exhibits rotational symmetry.
- Translation: When a figure is moved from one place to another without changing its orientation, it undergoes translational symmetry.
Regular Hexagons: Embodiments of Symmetry
Regular hexagons are captivating geometric shapes with six equal sides and six equal angles. They embody the essence of symmetry, possessing a remarkable six lines of symmetry. This extraordinary symmetry arises from their rotational symmetry of order 6, which means that if a regular hexagon is rotated by 60 degrees around its center, it will appear exactly the same.
Symmetry’s Influence on Regular Polygons
Symmetry has a profound influence on the properties of regular polygons. Because regular polygons, such as hexagons, have equal sides and angles, they possess inherent symmetry. This symmetry determines various characteristics, including:
- Angle Measures: The angles of regular polygons are always equal, with the measure of each angle determined by the number of sides.
- Side Lengths: Regular polygons have equal side lengths, ensuring a uniform shape.
- Area and Perimeter: The area and perimeter of regular polygons can be calculated using specific formulas that incorporate their symmetry.
Symmetry in geometry is a powerful force that brings order and beauty to the world of shapes. Its presence in regular hexagons, with their six lines of symmetry, underscores the significance of symmetry in defining the properties and aesthetics of geometric figures. By understanding the concept of symmetry and its impact on regular polygons, we gain a deeper appreciation for the intricate harmony that underlies our physical world.
Symmetry in Regular Polygons: Unveiling the Hidden Geometrical Harmony
In the captivating realm of geometry, symmetry reigns supreme as a fundamental principle that governs the beauty and order found within shapes. Regular polygons, such as hexagons, exemplify this concept, showcasing a remarkable balance and harmony that stems from their inherent symmetry.
General Properties of Regular Polygons
Regular polygons are geometric figures characterized by their equidistant sides and congruent angles. This inherent symmetry manifests in their uniform appearance, creating visually pleasing and aesthetically balanced forms. The number of sides and angles in a regular polygon is always equal, contributing to their symmetrical nature. For instance, a hexagon, as its name suggests, possesses six equal sides and six congruent angles.
Symmetry and Regular Polygons
Symmetry profoundly influences the properties of regular polygons, enhancing their structural integrity and aesthetic appeal. Rotational symmetry, in particular, plays a crucial role in shaping these polygons. Rotational symmetry refers to the ability of a figure to be rotated around a central point while maintaining its original appearance. Hexagons, for example, exhibit six lines of rotational symmetry, meaning they can be rotated six times around their center without altering their shape.
Exploring Rotational Symmetry
To understand rotational symmetry further, let’s delve into the concept of order. The order of rotational symmetry for a polygon is determined by the number of times it can be rotated while maintaining its original appearance. Regular hexagons have a rotational symmetry of order six because they can be rotated six times (60 degrees each time) before returning to their initial position. This rotational symmetry contributes to their symmetrical appearance and stability.
Regular polygons, such as hexagons, epitomize the harmonious interplay between symmetry and geometry. Their equal sides, congruent angles, and rotational symmetry create a sense of balance and visual appeal that captivates the eye. Understanding the principles of symmetry deepens our appreciation for the intricate beauty and order found within the world of shapes.