An octagon, an eight-sided polygon, has a sum of interior angles calculated using the formula (n – 2) x 180°, where n represents the number of sides. For an octagon (n = 8), the sum is (8 – 2) x 180° = 1080 degrees. This formula applies to any polygon, making it a versatile tool in geometry to determine angle measurements.
Understanding Octagons: A Geometrical Journey
In the realm of polygons, where shapes dance with angles and lines, there lies a fascinating figure known as the octagon. This geometrical marvel boasts eight sides, earning it its distinct name from the Greek words “octo” (eight) and “gon” (angle).
Beyond its simple definition, an octagon also possesses the characteristics of a quadrilateral, a polygon with four sides and four angles. This duality in its nature makes it a unique blend of geometrical concepts, offering insights into the intricate world of polygons.
So, let us embark on a journey to unravel the secrets of octagons, exploring their angles, their properties, and their significance in the realm of geometry.
Interior and Exterior Angles of Octagons: A Geometrical Distinction
Imagine an octagon, a fascinating polygon with eight straight sides and eight sharp corners. Nestled within the polygon’s framework lie interior angles, formed by pairs of adjacent sides, like two friends embracing. These interior angles are like secrets whispered between the sides.
On the other hand, exterior angles are the shy ones, formed by one side and the extension of its adjacent side. Picture an architect extending one side of the octagon, creating an angle that points outward, like a compass needle seeking the horizon.
Interior Angles: The Sum of Secrets
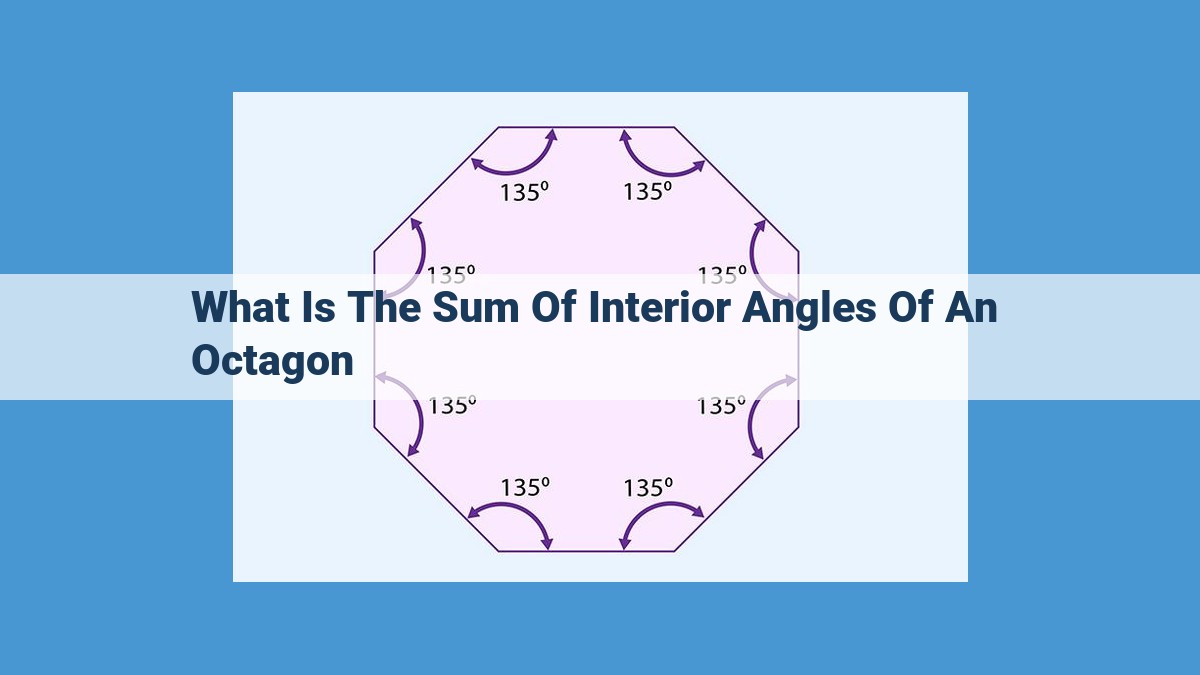
The sum of the interior angles of any polygon has a magical formula: (n – 2) x 180°, where n is the number of sides. For an octagon, with n = 8, the sum of its interior angles is 1080 degrees. It’s like a whisper chorus, where each angle contributes its share of 135 degrees to the harmonious total.
Exterior Angles: A Distant Chorus
Unlike their interior counterparts, exterior angles are not confined within the octagon’s boundaries. They extend outward, forming a secondary chorus. The sum of the exterior angles is always 360 degrees, regardless of the polygon’s shape. It’s a universal constant, like the rhythm of a heartbeat.
Regular Polygons and Angle Bisectors: Partners in Precision
In the realm of octagons, there’s a special type known as regular polygons, where all sides and angles are equal. In such polygons, angle bisectors play a crucial role. These lines divide interior angles into two equal parts, providing a key to unlocking the secrets of the octagon’s symmetry and harmony.
Unraveling the Enigma of Octagons: Interior Angles Unveiled
Embark on an intellectual odyssey as we delve into the fascinating realm of octagons. These enigmatic shapes, adorned with eight sides, beckon us to unravel their geometric intricacies. Like a master detective, we’ll scrutinize their angles, unlocking the secrets that lie within.
The Sum of Interior Angles: A Formulaic Revelation
At the heart of our exploration lies a formula that holds the key to the sum of interior angles in an octagon. Picture a polygon, any polygon, with n sides. The formula, (n – 2) x 180°, becomes our guiding light. It whispers the sum of interior angles, measured in degrees, like a gentle breeze carrying secrets.
For our octagon, with n equaling 8, the formula unveils a sum of 1080 degrees. This numerical gem represents the total measure of all eight interior angles, each one a piece of the geometric puzzle that forms this intriguing shape.
Implications of the Formula
This formulaic insight holds profound implications for octagons. Consider a regular octagon, where all sides and angles are equal. Armed with the sum of interior angles, we can effortlessly deduce the measure of each individual angle. The formula, like a master architect’s blueprint, reveals the hidden harmony and symmetry that defines these regular octagons.
Furthermore, the formula illuminates the relationship between interior and exterior angles. The exterior angle of an octagon, formed by one side and the extension of an adjacent side, is supplementary to the interior angle, meaning their sum equals 180 degrees. This geometric dance between interior and exterior angles adds another layer to the intrigue of octagons.
As we unravel the mysteries of octagons, their mathematical beauty unfolds before our eyes. The sum of interior angles, a cornerstone of geometric knowledge, unlocks a deeper understanding of these fascinating polygonal wonders. Embrace the journey of geometric discovery, where angles and sides intertwine in a captivating symphony of shapes.
Regular Polygons and Angle Bisectors: Unveiling the Secrets of Octagons
As we journey into the realm of polygons, let’s focus our attention on the enigmatic octagon, a shape with eight sides that holds a unique place in the geometric tapestry. In this blog post, we’ll delve into the fascinating aspects of regular octagons and uncover the significance of angle bisectors in understanding their properties.
What is a Regular Polygon?
A regular polygon is a shape characterized by equal sides and equal interior angles. Each angle within a regular polygon measures the same amount, offering a sense of symmetry and balance. An octagon, being a regular polygon with eight sides, exhibits this inherent symmetry.
The Role of Angle Bisectors
Angle bisectors play a pivotal role in unraveling the secrets of regular octagons. An angle bisector is a line segment that originates from the vertex of an angle and divides it into two equal parts. By studying angle bisectors, we can shed light on the individual interior angles of an octagon.
Determining Interior Angles
To determine the measure of each interior angle of a regular octagon, we employ the formula:
Interior Angle = Sum of Interior Angles / Number of Sides
For an octagon, the sum of interior angles is 1080 degrees, as calculated using the formula (n – 2) x 180°, where n represents the number of sides (8). Dividing 1080 by 8, we arrive at an interior angle measure of 135 degrees.
This means that each of the eight angles within a regular octagon measures 135 degrees, contributing to the overall symmetry and balance of the shape.
By unraveling the mysteries of regular octagons and the relevance of angle bisectors, we gain a deeper understanding of the geometric world around us. These concepts not only provide a foundation for further mathematical explorations but also offer insights into the harmonious relationships that exist within geometric shapes, both in nature and human-made structures.