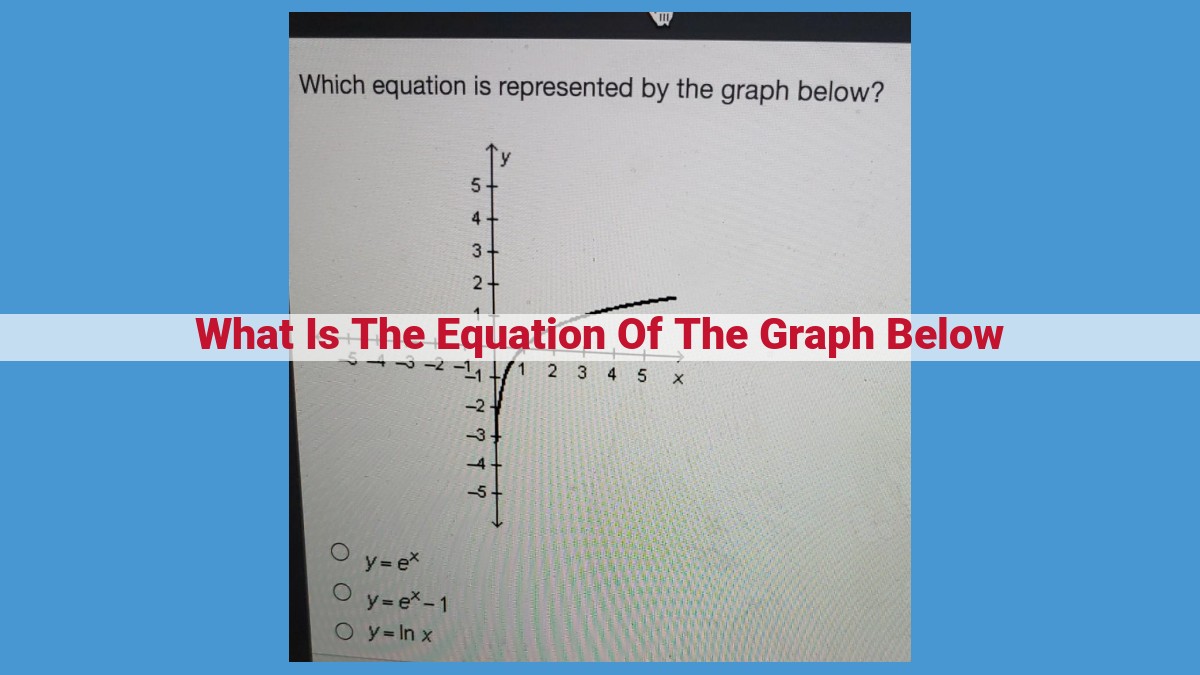
The equation of the graph is a linear equation, which is a mathematical expression that represents a straight line. It can be expressed in different forms, including point-slope form, slope-intercept form, and standard form. The slope of the line, represented by “m,” describes its steepness and the y-intercept, represented by “b,” is the point where the line intersects the y-axis. The equation of a linear line can be determined by its slope and y-intercept, or by extracting these values from its graph.
Unraveling the Essence of Linear Equations: A Beginner’s Guide
In the realm of mathematics, linear equations reign supreme as the building blocks of algebraic equations. They are simple yet powerful tools that describe straight lines on a graph. Understanding their anatomy and behavior is crucial for anyone embarking on a mathematical journey.
What is a Linear Equation?
A linear equation is an algebraic equation that represents a straight line on a graph. It is typically written in one of three forms:
- Slope-intercept form:
y = mx + b - Point-slope form:
y - y₁ = m(x - x₁) - Standard form:
Ax + By = C
Where:
* m represents the slope of the line
* b represents the y-intercept
* (x₁, y₁) represents a point on the line
* A, B, and C are constants
Essential Components: Slope and Y-Intercept
The slope of a line measures its steepness. It is calculated as the ratio of the change in y to the change in x along the line. A positive slope indicates an upward-sloping line, while a negative slope indicates a downward-sloping line. The y-intercept is the point where the line crosses the y-axis, indicating the line’s height at x = 0.
These components collectively define the unique characteristics of a linear equation, enabling us to understand and describe the behavior of straight lines on a graph.
Deconstructing Slope
- Explain the meaning of slope and its synonyms (rate of change, gradient).
- Discuss how slope describes the steepness of a line.
Deconstructing Slope: Understanding the Language of Lines
In the realm of algebra, linear equations hold a special place, describing straight lines that weave their way across the coordinate plane. One fundamental aspect of these lines is their slope, a numerical value that captures the line’s steepness and direction. But what exactly is slope, and how does it work?
Slope, often symbolized as “m,” is the rate of change in a line’s vertical direction relative to its horizontal movement. It measures the slant of the line, indicating how quickly it rises or falls as we trace along its path.
Think of a line as a hill. Its slope tells us how steep the hill is: a positive slope indicates an upward climb, while a negative slope represents a downward descent. The greater the slope’s absolute value, the steeper the hill. A slope of zero signifies a flat line, extending horizontally across the plane.
In everyday life, slope manifests itself in numerous contexts. For instance, when tracing the trajectory of a rolling ball, its slope indicates the ball’s speed and direction. In construction, slope is vital for designing roofs and ramps that are both functional and safe. And in finance, slope can reveal market trends and investment opportunities.
Understanding slope is crucial for deciphering the language of lines. It empowers us to not only describe lines but also to predict their behavior and solve a wide range of algebraic problems.
Identifying the Y-Intercept: The Line’s Gateway to the Y-Axis
In the realm of linear equations, the y-intercept holds a pivotal role in unraveling the equation’s secrets. It serves as the line’s gateway to the y-axis, where it paints a clear picture of the line’s position in the coordinate plane.
Defining the Y-Intercept
The y-intercept, denoted by the letter b in the slope-intercept form of a linear equation (y = mx + b), is the vertical point where the line intersects the y-axis. In simpler terms, it indicates the starting point of the line along the y-axis.
Significance of the Y-Intercept
The y-intercept reveals crucial information about the line’s behavior. It represents the line’s initial value when the x value is zero. For instance, in the equation y = 3x + 5, the y-intercept of 5 suggests that the line starts at a point 5 units above the origin on the y-axis.
Identifying the y-intercept empowers us to visualize the line without plotting the entire line. By simply knowing the y-intercept and the slope (m), we can quickly sketch the line’s path through the coordinate plane.
Constructing Lines with Point-Slope Form
- Introduce the point-slope form equation and explain its use in finding equations of lines passing through specific points.
Constructing Lines with Point-Slope Form: A Guide to Finding Equations Using Points
In the realm of mathematics, where precision reigns supreme, understanding the intricacies of linear equations is paramount. Among these equations, point-slope form stands as a valuable tool, empowering us to construct equations of lines that pass through specific points.
This form, defined as y – y1 = m(x – x1), connects the coordinates of a known point (x1, y1) with the slope (m) of the line. To unravel this equation’s power, let’s embark on a step-by-step journey.
Initially, locate a point on the line, acting as our reference point. This point will serve as a guidepost, anchoring our line in the coordinate plane. Next, determine the slope, which quantifies the line’s steepness and direction. Think of it as the angle the line forms with the horizontal axis.
With the point and slope in hand, the point-slope form equation becomes our guide. We plug in the coordinates of the point and the slope into the equation, creating a customized formula that perfectly fits our line.
For instance, suppose we have a line passing through the point (2, 3) with a slope of 2. Using the point-slope form, the equation becomes: y – 3 = 2(x – 2). This equation encapsulates the essence of the line, describing its path through the coordinate plane.
By leveraging the point-slope form, we gain the ability to construct equations for countless lines, connecting points and slopes with mathematical precision. This versatility makes it an indispensable tool for mathematicians, engineers, and anyone venturing into the world of linear equations.
Simplifying Slope-Intercept Form
- Introduce the slope-intercept form equation and explain its common usage in everyday applications.
Simplifying Slope-Intercept Form: A Convenient Way to Represent Lines
When it comes to linear equations, slope-intercept form stands out as a particularly convenient and widely used equation format. This form makes it easy to visualize and interpret the equation of a line, thanks to its straightforward structure.
The slope-intercept form equation takes the shape of y = mx + b, where:
yrepresents the dependent variable, or the value you’re solving forxrepresents the independent variable, or the value you’re plugging inmrepresents the slope, which describes the steepness of the linebrepresents the y-intercept, which is the point where the line crosses the y-axis
Everyday Applications
Slope-intercept form is a cornerstone of everyday applications involving linear equations. From modeling temperature changes to predicting financial trends, this equation form provides a clear and practical way to represent real-world scenarios.
For instance, in a weather forecast, the temperature over time can be modeled using a linear equation in slope-intercept form. The slope represents the rate at which the temperature changes, while the y-intercept gives the starting temperature. By plugging in different time values, we can predict the temperature at specific moments.
Simplifying the Form
Simplifying slope-intercept form involves isolating the y variable on one side of the equation. This process is essential for solving equations and understanding the relationship between x and y.
To simplify, we first subtract mx from both sides of the equation:
y - mx = b
Then, we rearrange the terms to get y alone:
y = b + mx
Slope-intercept form is an incredibly useful equation format that simplifies linear equations, making them easier to visualize and interpret. Whether you’re modeling real-world phenomena or solving everyday problems, understanding this form will empower you to navigate the world of linear equations with confidence.
Unraveling the Intricacies of Standard Form
In the realm of linear equations, standard form stands as a potent and widely employed equation format. Unlike its more familiar counterparts, slope-intercept and point-slope forms, standard form presents equations in a normalized manner, making it exceptionally useful for solving systems of equations and uncovering specific line properties.
The standard form equation takes the form Ax + By = C, where A, B, and C represent real numbers. These coefficients play a pivotal role in defining the line’s characteristics. The slope of the line is determined by the ratio -A/B, while the y-intercept is found by solving for C when x = 0.
Solving Systems of Equations
Standard form truly shines when it comes to solving systems of equations, which involve multiple equations and multiple variables. By equating the expressions of two standard-form equations, we can eliminate one variable, allowing us to solve for the other. This approach is far more efficient than attempting to solve systems using other equation forms.
Finding Equations of Lines with Specific Properties
Standard form also proves invaluable for finding the equations of lines that satisfy specific conditions. For instance, to find the equation of a line that passes through two given points, we can substitute the coordinates of those points into standard form and solve for the coefficients A, B, and C. Similarly, we can find the equation of a line that is parallel to another line or that has a specific slope or y-intercept.
Standard form is an indispensable tool for anyone delving into the world of linear equations. Its versatility in solving systems of equations and finding equations of lines with specific properties makes it an invaluable resource for students, researchers, and anyone who works with linear functions. Embracing standard form empowers us to tackle even the most complex linear equations with confidence and precision.
Visualizing the Graph of a Line
Unveiling the Line’s Secrets
Every line has an equation, and this equation holds the key to unlocking the line’s secrets. Just like a blueprint outlines a building, the equation of a line reveals its behavior, its direction, and its starting point.
The Story of a Line
Every line has a protagonist, a slope, that determines its steepness. A positive slope indicates an upward trend, as if the line is climbing a hill. Conversely, a negative slope signals a downward path, like a line descending a valley.
The line also has a y-intercept, like a starting gate for a race. This point marks where the line crosses the y-axis, the vertical number line. It tells us where the line begins its journey.
Building a Line from Scratch
With these two key players in place, it’s time to bring the line to life. Using the point-slope equation, we can construct a line that passes through a specific point and has a known slope. It’s like building a tower with a blueprint and some bricks.
Simplifying the Slope-Intercept Equation
Another common form of a line equation is the slope-intercept equation. Here, the slope and y-intercept are neatly packaged in a convenient format, much like a well-organized recipe. This form is widely used in real-world applications, such as modeling relationships between variables.
Finding the Equation from a Graph
But what if you only have a graph, not an equation? No worries! We can reverse-engineer the equation by studying the graph. By identifying the slope (the rise and run) and the y-intercept (where the line touches the y-axis), we can piece together the equation. It’s like solving a puzzle to uncover the hidden treasure.
Understanding the equation of a line is the key to unlocking its secrets and visualizing its path. By exploring the relationship between the equation and the graph, we gain a deeper insight into the world of linear relationships. So next time you encounter a line equation, remember this guide, and you’ll be able to decode its secrets like a master detective.
Extracting the Equation from a Graph: Unraveling the Line’s Story
Unveiling the equation that governs a line can be an intriguing journey that transforms a geometric sketch into a mathematical narrative. Let’s embark on this quest and discover how to extract the equation from a graph, revealing the hidden story it holds.
Determining Slope: The Line’s Inclination
The slope of a line, often denoted as “m,” describes its slant or steepness. It measures the rate at which the line ascends or descends. To determine the slope from a graph:
- Choose two distinct points on the line.
- Calculate the change in the y-coordinates between the points (known as “rise”).
- Divide the rise by the change in the x-coordinates between the points (known as “run”).
Identifying the Y-Intercept: The Line’s Crossing Point
The y-intercept is the point where the line intersects the y-axis, when x = 0. To identify the y-intercept from a graph:
- Locate the point where the line crosses the y-axis.
- Read the y-coordinate of this point. It represents the y-intercept, denoted as “b.”
Constructing the Equation: Putting It All Together
Once you have determined the slope (m) and the y-intercept (b), you can construct the equation of the line using the slope-intercept form:
y = mx + b
In this equation:
- y represents the dependent variable (the y-coordinate).
- x represents the independent variable (the x-coordinate).
- m is the slope.
- b is the y-intercept.
By plugging in the values of m and b, you can write the equation that precisely describes the line represented by the graph.