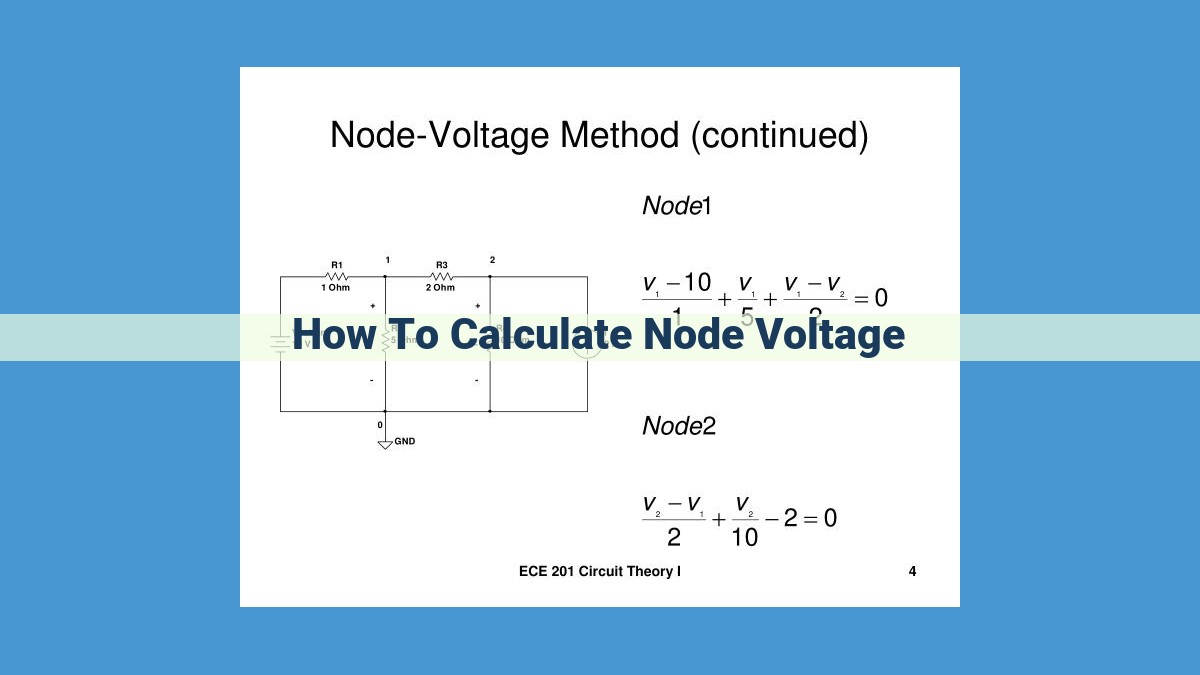
To calculate node voltage, apply Kirchhoff’s Voltage Law (KVL) to a closed loop that includes the node of interest. Calculate the sum of voltage drops around the loop by multiplying current through each resistor by its resistance. Set this sum equal to the algebraic sum of voltage sources in the loop. If multiple loops exist, write KVL equations for each loop and solve simultaneously using techniques like Superposition, Tellegen’s Theorem, or Nodal Analysis. By relating loop currents to node voltages, you can determine the voltage at each node.
Understanding Ohm’s Law: The Foundation of Circuit Analysis
- Explain the definition, mathematical expression, and relationship between resistance, voltage, and current.
- Provide examples of Ohm’s Law applications in simple circuits.
Understanding Ohm’s Law: The Foundation of Circuit Analysis
Ohm’s Law, a fundamental principle in electrical circuits, establishes a relationship between three crucial electrical quantities: voltage, current, and resistance. Named after the renowned physicist Georg Ohm, this law provides a cornerstone for understanding how these quantities interact and shape the behavior of circuits.
Ohm’s mathematical expression is concise and elegant: V = IR. This equation states that voltage (V) across a conductor equals the product of current (I) flowing through it and the resistance (R) of the conductor. The unit for voltage is volts, for current is amperes, and for resistance is ohms.
In simple circuits, Ohm’s Law helps us predict and manipulate electrical behavior. Consider a circuit with a battery (voltage source), a resistor, and a wire (negligible resistance) connecting them. Using Ohm’s Law, we can determine the current flowing through the circuit by dividing the battery voltage by the resistor resistance. Similarly, we can calculate the voltage across the resistor by multiplying its resistance with the current.
Ohm’s Law also assists in understanding electrical devices and their behavior in circuits. For instance, a resistor with a high resistance will restrict current flow, while a low-resistance resistor will allow more current to pass through. By incorporating Ohm’s Law into circuit analysis, engineers can design and optimize electrical systems across diverse applications.
Kirchhoff’s Voltage Law: Delving into the Secrets of Electrical Circuits
Imagine a network of electrical pathways, like a maze of interconnected wires and components. To decipher the mysteries of these circuits, we turn to Kirchhoff’s Voltage Law (KVL), a fundamental principle that guides us through the labyrinth.
KVL states that in any closed loop of a circuit, the algebraic sum of the voltage drops around the loop must be zero. This law is rooted in the conservation of energy, which dictates that energy cannot be created or destroyed.
Junctions: Where Electrical Paths Meet
At the heart of circuit analysis are junctions, intersections where multiple branches of the circuit meet. At each junction, current entering the junction must equal current leaving the junction, a phenomenon known as current conservation.
KVL and the concept of junctions empower us to venture into the depths of complex circuits. By identifying closed loops within the circuit, we can apply KVL to establish equations that relate the voltages around the loop. By solving these equations, we can determine the unknown voltages within the circuit, unlocking the secrets of its electrical behavior.
Real-World Applications of KVL
KVL finds widespread application in electrical engineering and circuit analysis. Engineers use it to:
- Design electrical circuits with optimal voltage distribution
- Troubleshoot faulty circuits by identifying voltage discrepancies
- Analyze the behavior of complex electronic systems, such as power grids and communication networks
Circuit Analysis Unveiled: Understanding Nodes, the Building Blocks of Electrical Networks
In the realm of electrical circuits, nodes play a pivotal role as connecting points where multiple branches converge. Imagine a bustling city, where busy streets intersect to form junctions. Nodes, like these junctions, are the key points in electrical circuits where branches meet.
Identifying Nodes: The Junctions of Circuits
Identifying nodes in circuits is crucial for understanding the flow of electrical signals. Look for points where multiple components, such as resistors, capacitors, or voltage sources, are connected. These points represent nodes, the meeting grounds of electrical paths.
Relationship with Meshes and Branches
Nodes are intricately connected to meshes and branches. Meshes are enclosed paths in a circuit, bounded by nodes, while branches are the individual segments of the circuit that connect nodes. The number of nodes in a circuit, minus one, equals the number of meshes.
Understanding Node Voltage: A Fundamental Concept
At each node in a circuit, the voltage is the same, a concept known as node voltage. This equality stems from the conservation of energy, as the energy flowing into a node through one branch must equal the energy flowing out through all other branches.
Understanding nodes is essential for mastering circuit analysis. These connecting points provide a framework for understanding how electrical signals navigate complex circuits. By identifying nodes and their relationship with meshes and branches, you gain a deeper comprehension of the intricate workings of electrical networks.
Voltage Divider Rule: Unveiling the Secrets of Series Circuits
When electrical components are connected in series, they form a pathway for current to flow through them sequentially. This arrangement not only affects the flow of current but also the distribution of voltage across the components. The voltage divider rule is a fundamental concept that helps us understand this phenomenon.
Voltage Divider Rule
The voltage divider rule states that in a series circuit, the voltage across each resistor is proportional to its resistance. Mathematically, it can be expressed as:
Vr = V * Rr / Rt
where:
- Vr is the voltage across the resistor
- V is the total voltage across the series circuit
- Rr is the resistance of the resistor
- Rt is the total resistance of the circuit
How it Works
Imagine a series circuit with two resistors, R1 and R2. When a voltage source is connected across the circuit, the current flowing through both resistors is the same. However, the voltage distribution across the resistors is not equal.
The resistor with the higher resistance will have a higher voltage drop across it. This is because resistance opposes the flow of current, causing a greater voltage to be lost across the resistor with a higher resistance.
Applications
The voltage divider rule has numerous applications in electrical circuits, such as:
- Controlling voltage levels in different parts of a circuit
- Creating voltage references
- Biasing transistors
- Designing passive filters and voltage regulators
Derivation
The voltage divider rule can be derived from Ohm’s law. Ohm’s law states that the voltage across a resistor is directly proportional to the current flowing through it and its resistance. In a series circuit, the current is the same through all resistors, so the voltage across each resistor is proportional to its resistance.
The voltage divider rule is a powerful tool for analyzing and understanding series circuits. It allows us to calculate the voltage distribution across resistors and design circuits with specific voltage requirements. When combined with Ohm’s law and other circuit analysis techniques, it provides a comprehensive understanding of electrical circuits.
The Superposition Theorem: A Lifeline for Circuit Analysis
Navigating the complexities of electrical circuits can be a daunting task, but fear not! The Superposition Theorem is here to simplify the labyrinth, providing a clear path to understanding even the most intricate of circuits.
The Superposition Theorem is a powerful tool that allows us to analyze linear circuits by breaking them down into their constituent parts. In a linear circuit, the relationship between voltage, current, and resistance remains proportional, making it possible to isolate and analyze each source individually.
Step 1: Divide and Conquer
The first step is to transform each voltage or current source into an equivalent circuit. This involves replacing the source with either a short circuit (for voltage sources) or an open circuit (for current sources). By doing so, we effectively remove the influence of all other sources in the circuit.
Step 2: Calculate Individual Responses
With the sources isolated, we can calculate the response of the circuit to each source independently. This involves determining the voltage at a specific node or the current through a particular branch.
Step 3: Superimpose the Responses
The final step is to superimpose the individual responses to determine the overall response of the circuit. Simply add the voltage or current values obtained from each source to find the total result.
Real-World Applications
The Superposition Theorem has countless applications in the world of electrical engineering, from power system analysis to electronic circuit design. It empowers engineers to solve complex circuits efficiently and accurately, ensuring the proper functioning of everything from our homes to our industries.
Embrace the Superposition Theorem, and unlock the mysteries of electrical circuits. It’s a key that opens doors to a deeper understanding, simplifying the complex and illuminating the path to circuit analysis mastery.
Thevenin’s Theorem: Creating Equivalent Circuits
- Introduce Thevenin’s Theorem and its utility.
- Explain how to transform circuits into equivalent circuits using Thevenin’s equivalent voltage and resistance.
- Demonstrate how to calculate node voltage using Thevenin’s theorem.
Thevenin’s Theorem: Simplifying Circuit Analysis
In the world of electrical circuits, complexity can often become a daunting hurdle. However, Thevenin’s Theorem emerges as a savior, providing a powerful tool to simplify complex circuits and make their analysis a breeze. This theorem allows us to create equivalent circuits that represent the original circuit in a much simpler form.
Imagine a complex circuit with multiple components and branches intertwined like a tangled web. Thevenin’s Theorem transforms this maze into a simple two-terminal network consisting of a voltage source and a series resistor. This equivalent circuit captures the behavior of the original circuit at a specific pair of terminals.
To derive the Thevenin equivalent, we first identify the terminals of interest. Then, we follow these simple steps:
-
Calculate the Thevenin’s Equivalent Voltage (Vth):
- Disconnect the terminals from the original circuit.
- Calculate the voltage (Voc) between the terminals using any appropriate method (e.g., voltage divider rule).
-
Calculate the Thevenin’s Equivalent Resistance (Rth):
- Short-circuit the terminals (i.e., connect them together).
- Measure the resistance (Rsc) between the terminals.
With these values, we can now construct the Thevenin equivalent circuit: a voltage source Vth in series with a resistor Rth. This equivalent circuit can be used to analyze the original circuit, making it much easier to calculate node voltages and other circuit parameters.
Norton’s Theorem: Unveiling an Alternative Source Transformation
In the realm of circuit analysis, where understanding the intricacies of electrical networks is paramount, Norton’s Theorem emerges as a fundamental tool. It offers an alternative perspective to Thevenin’s Theorem, providing a different yet equally effective approach to simplify and analyze complex circuits.
Like Thevenin’s Theorem, Norton’s Theorem transforms a circuit into an equivalent circuit with a voltage source in series with a resistance. However, the key distinction lies in the transformed source’s nature. Norton’s Theorem utilizes a current source instead of a voltage source.
Delving into the Similarities and Differences
Both Norton’s Theorem and Thevenin’s Theorem aim to simplify complex circuits by replacing them with simpler equivalents. However, their source transformations differ. Thevenin’s equivalent circuit** has a _voltage source, while Norton’s equivalent circuit employs a current source.
Transforming Circuits with Norton’s Approach
Norton’s Theorem transforms circuits through a three-step process. Firstly, it disables all sources in the circuit, maintaining the other components. Secondly, it calculates the output current flowing through an ideal voltage source connected across the open circuit. This current is known as the Norton’s equivalent current (In)_. Finally, it measures the resistance between the circuit’s output terminals with the sources disabled. This resistance is known as the Norton’s equivalent resistance (Rn).
Determining Node Voltage with Norton’s Equivalent Circuit
Once the Norton’s equivalent circuit has been established, it can be used to determine node voltage. The current source and resistor are connected in series, and the new circuit is connected to the external circuit. The voltage across the external circuit is the same as the voltage across the Norton’s equivalent resistor. This voltage can be calculated using Ohm’s Law:
V = In * Rn
where:
- V is the voltage across the external circuit
- In is the Norton’s equivalent current
- Rn is the Norton’s equivalent resistance
Unlocking the Power of Norton’s Theorem
Norton’s Theorem is particularly useful when dealing with complex circuits or circuits with multiple sources. It simplifies circuit analysis by reducing the circuit to a simpler equivalent circuit. This makes it easier to analyze circuit behavior and calculate node voltage.
By understanding and applying Norton’s Theorem, circuit analysts can effectively simplify complex circuits and gain a deeper understanding of electrical networks.