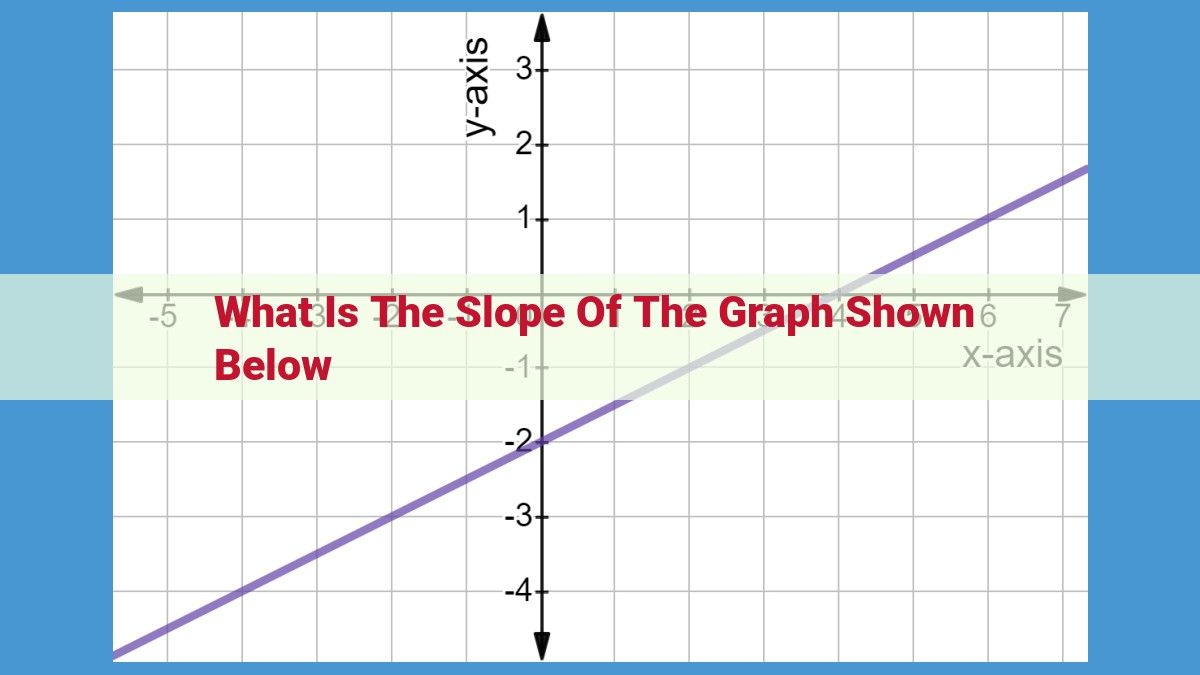
The slope of a graph measures the steepness of a line. It is calculated as the change in y-coordinates (y2 – y1) divided by the change in x-coordinates (x2 – x1). Horizontal lines have a zero slope, indicating no change in height, while vertical lines have an undefined slope as they do not have a defined x-coordinate difference. Lines with positive slopes rise from left to right, while those with negative slopes fall from left to right. Understanding slope is crucial for interpreting data and analyzing trends visualized on graphs.
Navigating the Slopes of Life: An Exploratory Guide
Have you ever wondered why some hills seem more challenging to climb than others? Or why a rollercoaster’s steep drop leaves you breathless? The answer lies in slope, a measure of the steepness of a line. In this blog, we’ll embark on a journey to understand slope and its significance in our everyday lives.
As we begin our ascent, let’s first define slope. Slope measures the steepness or inclination of a line. It tells us how much the line rises (or falls) for every unit it moves horizontally. Imagine a road winding up a mountain; the steeper the road, the greater the slope.
Now, let’s consider two special types of lines: horizontal lines and vertical lines. Horizontal lines run parallel to the ground (x-axis), so they have a slope of zero. Vertical lines, on the other hand, shoot straight up (y-axis) and have an undefined slope. This is because they don’t “rise” or “run” horizontally, making it impossible to calculate a slope.
Understanding Graphs: Slope and Trends
When we look at the world around us, we often see patterns and trends. These patterns can be represented visually using graphs, which allow us to identify key relationships between variables. One important aspect of graphs is the slope of lines, which tells us how steep the line is and provides valuable insights into the data it represents.
Visualizing Data with Graphs
Graphs are powerful tools for presenting data in a way that makes it easy to understand. By plotting points on a two-dimensional surface, we can create lines that represent the trends and relationships between different variables. The x-axis of a graph typically represents the independent variable (what we are changing), while the y-axis represents the dependent variable (what is being affected).
Different Types of Lines: Positive and Negative Slopes
Lines on a graph can have different slopes, which describe their steepness and direction. A line with a positive slope is rising from left to right, while a line with a negative slope is falling from left to right. The magnitude of the slope indicates how steep the line is: a steeper line has a higher slope value.
In many real-world scenarios, positive and negative slopes can represent different relationships between variables. For example, in a graph showing the relationship between temperature and time, a positive slope would indicate that the temperature is increasing over time, while a negative slope would indicate that the temperature is decreasing over time.
By understanding the slope of lines on graphs, we can gain valuable insights into the data they represent. Slope helps us identify trends, predict future values, and compare relationships between different variables. Understanding slope is a fundamental skill in data analysis and interpretation, enabling us to make informed decisions based on the information presented in graphs.
Delving into the Enigma of Slope: A Journey of Understanding and Calculation
Comprehending the Concept
Before venturing into the depths of calculating slope, let’s unravel its essence. Envision a mountain, its towering peaks and sloping sides. These slopes depict the steepness of the terrain. Similarly, in mathematics, slope serves as a measure of the steepness of a line. It quantifies the slant of a line compared to the horizontal axis.
The Intriguing World of Graphs
Graphs are our visual guides to the world of data and lines. They make patterns and relationships tangible, allowing us to discern trends and behaviors. Lines on graphs come in various slopes:
- Positive Slopes: Upsloping lines that rise from left to right, indicating a positive relationship between the x- and y-coordinates.
- Negative Slopes: Downsloping lines that fall from left to right, suggesting an inverse relationship between x and y.
Unveiling the Slope Formula
Now, let’s embark on the journey of calculating slope. The secret lies in the slope formula:
Slope = (y2 - y1) / (x2 - x1)
where:
- y1 and x1 represent the coordinates of one point on the line
- y2 and x2 represent the coordinates of another point on the line
This formula embodies the essence of slope: it captures the change in the y-coordinate relative to the change in the x-coordinate.
Guiding Example: Unraveling Slope from a Graph
Imagine a line on a graph, elegantly connecting points A (2, 1) and B (4, 3). To calculate its slope, we invoke the slope formula:
Slope = (y2 - y1) / (x2 - x1)
Substituting the coordinates:
Slope = (3 - 1) / (4 - 2)
Slope = 2 / 2
Slope = 1
Our exploration reveals that this line slopes upward with a gradient of 1.
Horizontal and Vertical Lines: Special Slope Cases
However, not all lines conform to the typical slope formula. When a line runs parallel to the horizontal axis, it has a zero slope. This is because the change in y is zero, despite any change in x. Conversely, lines that run parallel to the vertical axis have an undefined slope. This is because the change in x is zero, making the slope formula indeterminate.
Comprehending slope is a fundamental skill in the realm of mathematics and beyond. It empowers us to decode the behavior of lines, discern patterns, and unravel the underlying relationships within data. Whether on graphs or in the real world, understanding slope unlocks a wealth of insights into our surroundings.
Horizontal and Vertical Lines: A Tale of Two Slopes
In the realm of geometry, lines dance across the page, revealing patterns and insights. Among these lines, horizontal and vertical lines stand out as special entities, each possessing a unique slope.
Horizontal lines, like patient rulers, stretch across the plane without ever deviating from their level path. Their slope, a measure of their inclination, is zero. Imagine a lazy river meandering through a meadow, its water gliding smoothly along a horizontal line.
Vertical lines, on the other hand, stand tall and unyielding, perpendicular to the horizon. Their slope is undefined, for they rise straight up without any discernible slant. Think of a skyscraper piercing the clouds, its walls soaring vertically without a hint of incline.
This difference in slope has profound implications for the behavior of these lines. Horizontal lines, with their zero slope, never change in height as they extend indefinitely. They parallel the x-axis, remaining at the same level throughout their journey.
Vertical lines, with their undefined slope, mark a sharp divide on the plane. They intersect the y-axis at a single point, forming a boundary that separates different regions. Their height increases without bound as they reach towards infinity.
In essence, horizontal lines represent constant values, while vertical lines represent infinite gradients. They serve as indispensable tools for visualizing data, identifying trends, and solving geometric problems. Understanding their unique properties is essential for navigating the world of lines and unlocking their mathematical secrets.
Understanding Slope: A Guide to Measuring Steepness
What is Slope?
Slope is a mathematical concept that measures the steepness of a line. It describes how much a line rises or falls along the vertical axis (y-axis) compared to its horizontal movement along the horizontal axis (x-axis).
Horizontal and Vertical Lines: Undefined Slopes
Horizontal lines run parallel to the x-axis, neither rising nor falling. As such, they have zero slope. In contrast, vertical lines run parallel to the y-axis, rising or falling infinitely. Therefore, they have undefined slope, as there is no horizontal movement to compare.
Graphs and Slope
Graphs are powerful tools for visualizing data and identifying trends. Different types of lines represent different slopes:
- Lines sloping upwards from left to right have positive slopes.
- Lines sloping downwards from left to right have negative slopes.
Calculating Slope
The slope of a line can be calculated using the formula:
Slope = (change in y) / (change in x)
Where:
- Change in y = y2 – y1 (difference in vertical coordinates of two points on the line)
- Change in x = x2 – x1 (difference in horizontal coordinates of two points on the line)
Example: Calculating Slope from a Graph
Consider a line passing through points (2, 1) and (4, 3). Using the slope formula:
Slope = (3 - 1) / (4 - 2)
Slope = 2 / 2 = **1**
Therefore, the slope of the line is 1.
Slope is a key concept in understanding the behavior of lines. By understanding slope, we can determine the steepness and direction of lines, which are invaluable in various fields such as mathematics, physics, and economics.