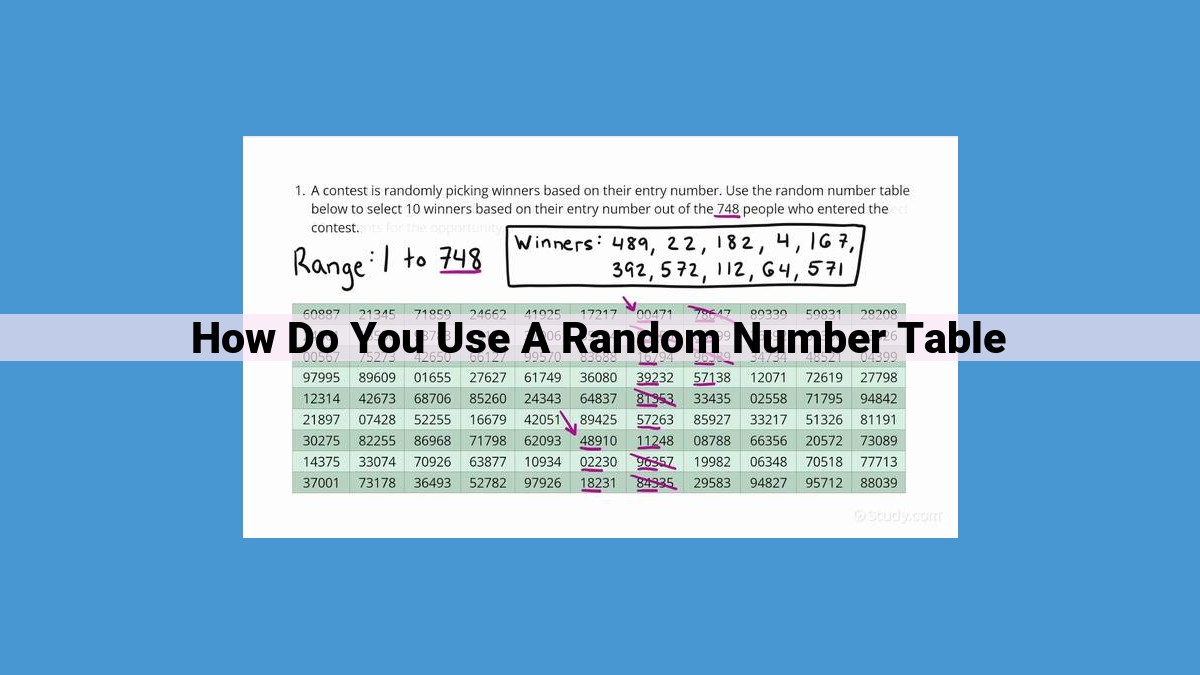
To use a random number table, start by identifying the heading (starting point) and establish a sampling interval (number of digits to skip between selections). Locate the heading and move through the table based on the interval, extracting blocks of digits. These extracted blocks represent random numbers that can be assigned to participants, selected for experiments, or used in statistical analysis. By following this process, you can ensure fair and unbiased outcomes in various applications such as choosing winners, selecting subjects, and generating samples for data collection.
Unlocking the Power of Randomness: A Comprehensive Guide to Random Number Tables
In the world of data and analysis, where precision and accuracy reign supreme, randomness holds a pivotal role. Random number tables serve as indispensable tools for introducing this crucial element into various research and application scenarios.
What are Random Number Tables?
Random number tables are meticulously crafted collections of digits generated using statistical methods to ensure unpredictability and randomness. These tables find widespread use in fields such as sampling, experimentation, and data analysis.
Construction of Random Number Tables
The construction of random number tables is a meticulous process that involves sophisticated algorithms and rigorous quality control. These tables are typically arranged in columns and rows, with each block of digits representing a unique random number.
Components of Random Number Tables
Heading: The starting point of a random number sequence.
Columns and Rows: The divisions that organize the table into blocks of digits.
Block: A group of digits designated by a line or space, representing a single random number.
Generating Random Numbers from a Table
To extract random numbers from a table, you need to define the sampling interval, which is the number of digits skipped between each selected number. The heading provides the initial starting point for the sequence.
By combining the heading and sampling interval, you can generate a series of random numbers that meet specific requirements.
Sampling Techniques with Random Number Tables
Random number tables enable scientific sampling techniques, where a representative portion of a population is selected for study. The sampling interval ensures that the selection process remains unbiased and random.
By applying sampling intervals, researchers can select subjects or data points from a larger population without introducing any systematic bias.
Practical Applications of Random Number Tables
The applications of random number tables extend far beyond the realm of theoretical statistics. They play a vital role in:
- Choosing Winners: Random numbers are assigned to participants to ensure fairness in selection.
- Scientific Experiments: Subject allocation for experiments is randomized to minimize experimental bias.
- Statistical Analysis: Random samples are generated for data collection, ensuring unbiased and representative results.
Randomization is an essential tool for researchers and statisticians, allowing them to eliminate bias and draw valid conclusions from their data. Random number tables provide a practical and reliable means of introducing randomness into sampling and data analysis processes.
By understanding the concepts and applications of random number tables, you can harness their power to enhance the accuracy and validity of your research and decision-making.
Components of a Random Number Table
- Heading: The starting point of a random number sequence
- Columns and Rows: How the table is divided into blocks of digits
- Block: A group of digits designated by a line or space
Understanding the Components of a Random Number Table
Random number tables, essential tools in various fields from statistics to gambling, provide sequences of seemingly unpredictable digits that form the foundation of many data-driven processes. Understanding their components is crucial for using them effectively.
Heading: The Gateway to Randomness
At the genesis of each random number table lies the heading. This starting point is a random number assigned to initiate the sequence. It serves as the gateway into a labyrinth of digits, paving the path for the unpredictable journey that follows.
Columns and Rows: A Grid of Digits
The table is meticulously divided into columns and rows, creating a grid-like structure. These divisions segment the vast number of digits into manageable blocks, making it easier to navigate and decipher.
Block: Grouping Digits with Purpose
Within the table, blocks are groups of digits clearly marked by lines or spaces. Each block represents a unique sequence generated from the heading using mathematical algorithms. The block size varies depending on the table’s design, typically ranging from 5 to 10 digits.
Random Number Generation from a Table
In the world of data and decision-making, randomness plays a crucial role in ensuring fairness and objectivity. Random number tables are a powerful tool that allow us to generate truly random numbers for a wide range of applications. Understanding how to generate random numbers from a table is essential for unlocking their utility.
What are Random Numbers?
Random numbers are numbers that have no predictable pattern or bias. They are generated through a process that ensures that each number has an equal chance of being selected. This unpredictability is what makes random numbers so valuable in various fields, such as statistical analysis, scientific experiments, and even games of chance.
Methods for Generating Random Numbers
Using a random number table, you can generate random numbers by selecting a starting point, known as the heading, and a sampling interval. The sampling interval represents the number of digits you skip between each number you choose.
To generate a random number:
- Choose a heading: Randomly select a point within the table by closing your eyes and pointing your finger. The number at that point becomes your heading.
- Determine your sampling interval: Decide how many digits you want to skip between each selected number. For example, if you choose a sampling interval of 2, you will skip every other digit.
- Move through the table: Starting from the heading, count along the row or column by the sampling interval, selecting every digit as you go.
- Record your random numbers: Note down the digits you select. Ensure you skip the corresponding number of digits according to your sampling interval.
By following these steps, you can generate a sequence of truly random numbers that can be used for various purposes.
Sampling Techniques with Random Number Tables
In the realm of statistics and research, randomization plays a crucial role in ensuring unbiased outcomes. One tool that aids in this process is the random number table.
The Concept of Sampling
Sampling involves selecting a representative portion of a population to gather data and draw inferences about the entire group. Random number tables are particularly useful in sampling because they generate unpredictable sequences of digits that can be used to identify specific individuals or data points.
Sampling Interval
The sampling interval refers to the number of digits skipped between each selected number. This interval is determined based on the population size and the desired sample size. By systematically skipping digits, researchers aim to avoid any bias or pattern that could skew the sample.
Example of Random Sampling
Consider a research study that requires selecting 50 participants from a population of 500. Using a random number table with a heading of 0123 and a sampling interval of 10, the researcher would start at 0123 and select every 10th digit that follows. This process would yield a random sample of 50 participants that is representative of the entire population.
Additional Points to Note:
- Starting Point: The starting point for selecting numbers is determined by the random number heading provided in the table.
- Block Size: The size of each block in the table typically consists of multiple digits, often 5 or 10.
- Reliability: Random number tables are highly reliable as they are constructed using rigorous mathematical algorithms or physical processes to ensure unpredictability.
- Alternatives: In addition to physical tables, there are also computer-generated random number generators available, offering a convenient and equally reliable option.
Practical Applications of Random Number Tables: Unlocking Fairness and Accuracy
In the realm of statistics and experimentation, randomness plays a pivotal role in ensuring impartiality and preventing bias. Random number tables serve as powerful tools to generate sequences of unpredictable numbers, enabling researchers and practitioners to make impartial selections and draw representative samples.
One prominent application of random number tables is in choosing a winner in contests or raffles. By assigning unique random numbers to each participant, organizers can eliminate human bias and guarantee a fair and transparent selection process. The winner is randomly chosen by selecting a number from the table and matching it to the corresponding participant.
In the world of scientific experiments, random number tables play a crucial role in selecting subjects. Researchers use these tables to ensure that the subjects chosen for their studies are representative of the population they are investigating. By randomly selecting subjects, researchers can avoid introducing bias and ensure that their findings are generalizable to the larger population.
Statistical analysis is another area where random number tables are indispensable. Researchers use these tables to generate random samples of data for various analyses. By selecting a subset of data using random numbers, statisticians can ensure that their samples are representative of the larger population, leading to more accurate and reliable conclusions.
In summary, random number tables are essential tools for introducing randomness and eliminating bias in a wide range of applications, from selecting contest winners to designing scientific experiments and conducting statistical analyses. Their ability to generate unpredictable sequences of numbers ensures fairness, impartiality, and the accuracy of results.