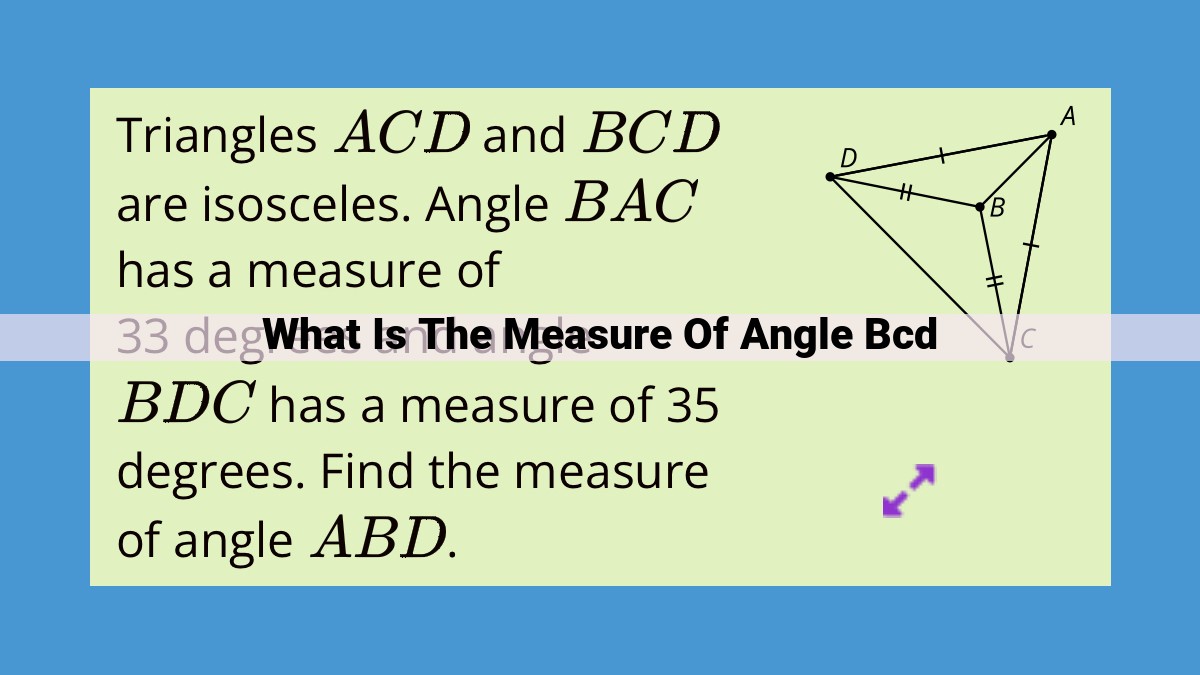
This article focuses on determining the measure of angle BCD. It begins by defining angles and their importance in geometry. The article then explains supplementary angles, linear pairs, and the angle addition postulate. Using these concepts, it shows how to determine the measure of angle BCD based on the given information. The final answer is explained and its significance is discussed. The article concludes by summarizing the concepts learned and reiterating the measure of angle BCD.
Determining the Measure of Angle BCD: A Geometric Journey
Welcome to the fascinating world of geometry, where angles play a pivotal role. Angles are formed by the intersection of two lines or rays, and they determine the shape and size of objects.
Our mission today is to embark on a geometric adventure to unravel the measure of angle BCD. This exciting quest will take us through the realms of supplementary angles, linear pairs, and the angle addition postulate.
Along the way, we’ll discover the secrets that unlock the mystery of angle BCD. So, buckle up and get ready for an unforgettable trip into the enigmatic realm of geometry!
Supplementary Angles
- Define supplementary angles (sum to 180 degrees).
- Describe situations where supplementary angles occur.
- Mention related concepts: complementary angles, vertical angles, and adjacent angles.
Supplementary Angles: A Journey into the World of Angle Relationships
In the world of geometry, understanding angles and their relationships is a key to unlocking a treasure trove of knowledge. Among the many types of angle relationships, supplementary angles hold a special place. They are like two halves of a puzzle, fitting together perfectly to create a whole of 180 degrees.
What are Supplementary Angles?
Supplementary angles are defined as angles that add up to 180 degrees. Imagine two lines intersecting to form two adjacent angles. If these angles have a sum of 180 degrees, they are considered supplementary. We can also think of supplementary angles as two angles that together form a straight line.
Where Do Supplementary Angles Occur?
Supplementary angles show up in numerous scenarios in geometry. Here are a few examples:
- Adjacent angles that form a straight line: When two lines intersect to form adjacent angles that add up to 180 degrees, the angles are supplementary.
- Vertical angles: Vertical angles are opposite angles formed by intersecting lines. These angles are always supplementary, meaning their sum is 180 degrees.
- Linear pairs: A linear pair is a pair of adjacent angles that form a straight line. By definition, linear pairs are supplementary.
Related Concepts
Understanding supplementary angles requires familiarity with a few related concepts:
- Complementary angles: Complementary angles are angles that add up to 90 degrees.
- Vertical angles: As mentioned earlier, vertical angles are opposite angles formed by intersecting lines. They are always supplementary to each other.
- Adjacent angles: Adjacent angles share a common side and a common vertex. Supplementary angles are a specific type of adjacent angles that add up to 180 degrees.
Supplementary angles are an essential concept in geometry. They are defined as angles that add up to 180 degrees. Understanding supplementary angles and their relationships helps in solving problems involving angles and geometric figures. Familiarizing with complementary angles, vertical angles, and adjacent angles further enhances our understanding of angle relationships in the mathematical world.
Linear Pairs: Supplementary Angles on a Straight Line
In the realm of geometry, angles play a crucial role in defining shapes and measuring relationships. Among the various types of angles, there exists a special duo known as supplementary angles. These are angles that, when combined, form a straight line, creating a total measure of 180 degrees.
A linear pair is a unique type of supplementary angle formed when two adjacent angles share a common vertex and a common side. In simpler terms, they are supplementary angles that sit side-by-side on a straight line.
To illustrate, imagine two rays originating from a single point, forming two angles that extend in opposite directions. If these angles sum up to 180 degrees, they form a linear pair.
Linear pairs are of great importance in geometry as they provide a foundation for understanding various angle relationships. They are closely associated with adjacent angles, which share a common vertex and one common side. When two adjacent angles form a linear pair, they are often referred to as consecutive or adjacent supplementary angles.
Vertical angles are another type of angle that relates to linear pairs. They are formed when two intersecting lines create four angles. The angles opposite each other are known as vertical angles, and they possess a unique property: they are always congruent, meaning they have the same measure.
In conclusion, linear pairs are a fascinating aspect of angle relationships in geometry. They are supplementary angles that form a straight line, and they are closely intertwined with adjacent angles and vertical angles. Understanding linear pairs is essential for solving geometry problems and appreciating the intricacies of angle measurements.
Angle Addition Postulate
- State the angle addition postulate (sum of measures of adjacent angles equals the larger angle).
- Provide examples of the angle addition postulate in action.
- Mention related concepts: segment addition postulate, triangle inequality theorem, and Pythagorean theorem.
The Angle Addition Postulate: Unveiling the Secrets of Angles
In the realm of geometry, angles hold a pivotal role, shaping the very fabric of geometric figures. Understanding angles and their properties is paramount for unraveling the mysteries of this fascinating subject.
The Angle Addition Postulate stands among the cornerstones of angle relationships. It proclaims that the sum of the measures of two adjacent angles equals the measure of the larger angle. This postulate provides a cornerstone for proving properties of triangles, quadrilaterals, and other geometric figures.
Picture this: You have two angles, let’s call them Angle A and Angle B, that share a common vertex and lie side by side. The Angle Addition Postulate tells us that the measure of the larger angle, say Angle A, is equal to the sum of the measures of the smaller angles, Angle A and Angle B.
For instance, if Angle A measures 70 degrees and Angle B measures 30 degrees, then Angle A would be the larger angle with a measure of 100 degrees. The Angle Addition Postulate beautifully captures this relationship, indicating that Angle A equals Angle A + Angle B.
Moreover, the Angle Addition Postulate finds kinship with other important geometric postulates. The Segment Addition Postulate asserts that the length of a line segment is equal to the sum of the lengths of its parts. The Triangle Inequality Theorem proclaims that the sum of the lengths of two sides of a triangle must be greater than the length of the third side. And the Pythagorean Theorem establishes the relationship between the lengths of the sides of a right triangle.
These postulates, including the Angle Addition Postulate, form an interconnected web that reveals the fundamental truths of geometry. They equip us with the tools to navigate the intricate landscape of angles and unravel the secrets that lie within.
Determining the Measure of Angle BCD
In the realm of geometry, angles play a pivotal role, shaping the very fabric of figures and unraveling the mysteries of their measurements. Among the multitude of angles, we embark on a journey to unveil the hidden measure of angle BCD, a key element in unlocking the secrets of geometrical puzzles.
Our quest begins by understanding supplementary angles, angles that dance harmoniously, summing up to 180 degrees. Like partners in a perfect waltz, they gracefully complement each other, creating a straight line as their united path. This harmonious union often manifests in adjacent angles, angles that share a common vertex and a side, or in vertical angles, angles formed by intersecting lines.
Next, we delve into the realm of linear pairs, supplementary angles that ascend to a higher level, forming a straight line, a geometric masterpiece where two lines gracefully intertwine. Their bond is unbreakable, as they share both a vertex and all their sides, mirroring each other like twins.
Armed with these concepts, we invoke the wisdom of the Angle Addition Postulate, a guiding principle that proclaims the sum of measures of adjacent angles equals the larger angle. Like a wise mentor, it guides us toward the truth, revealing the hidden secrets of angles.
Now, let us apply this knowledge to our quest, the elusive angle BCD. Imagine a geometric landscape, where angles dance and measures hide in plain sight. We are given tantalizing clues: angle ABE measures 40 degrees, and angle EBD is a supplementary angle to angle ABE.
With these clues, we can paint a picture of the geometric dance. Angle ABE and angle EBD form a harmonious linear pair, their measures adding up to 180 degrees. Using the Angle Addition Postulate, we can deduce that angle EBD measures 180 degrees – 40 degrees = 140 degrees.
But our journey does not end here. Angle BCD is a sly angle, hiding its measure behind a veil of supplementary angles. However, we know that angle ABE and angle BCD are also a linear pair. Thus, angle BCD must also measure 140 degrees.
And so, we have unmasked the secret of angle BCD, its measure revealed to be 140 degrees. This discovery serves as a testament to the power of geometry, where concepts intertwine like threads in a tapestry, leading us to the heart of mathematical understanding.