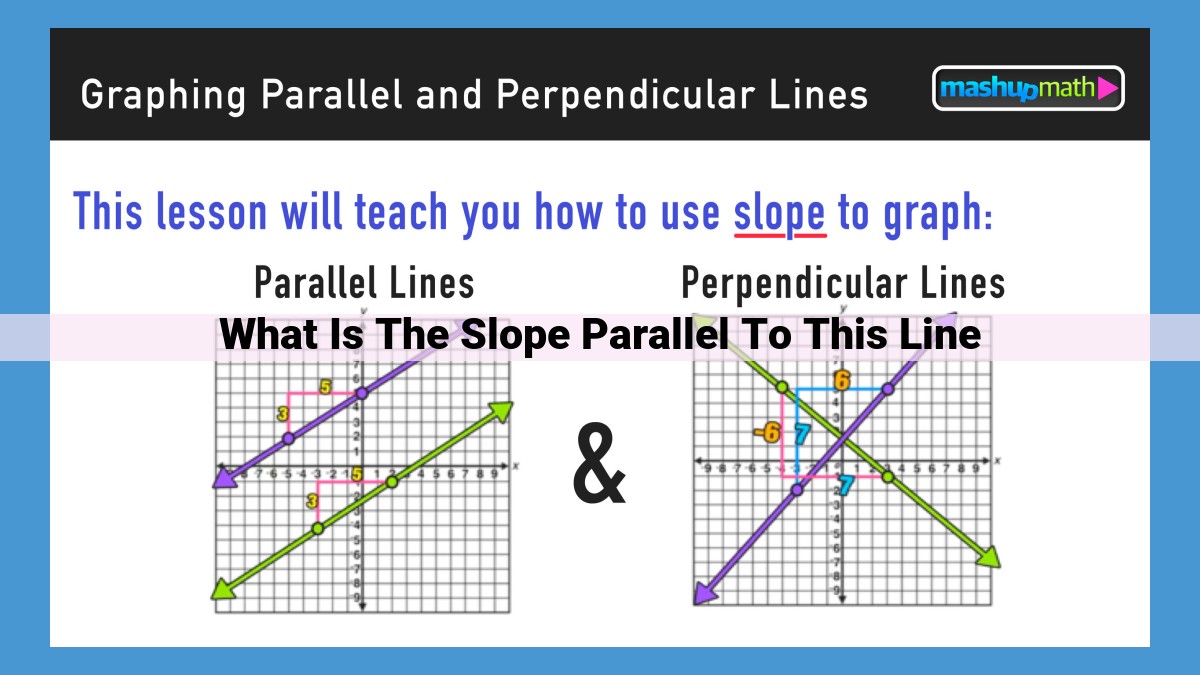
Parallel lines share the same slope, a measure of their steepness. The slope of a line is the ratio of its vertical to horizontal change, represented by the slope-intercept form (y = mx + b), where ‘m’ represents the slope. To find the slope of a line parallel to a given line, determine the slope of the given line and use the same value. Parallel lines never intersect and maintain equal slopes, making them crucial for applications in construction, architecture, and other fields where precise alignment is essential.
Understanding Slope and Parallel Lines: A Journey into Geometry
In the realm of geometry, slopes play a pivotal role in describing the steepness of lines, while parallel lines are like kindred spirits, sharing a harmonious bond. Let’s embark on an adventure to unravel their intriguing characteristics.
Slope: The Measure of Line Steepness
Imagine a line traversing a landscape, rising and falling as it moves. The slope of this line quantifies its inclination—how sharply it ascends or descends. It’s defined as the ratio of the line’s vertical change (the difference in y-coordinates) to its horizontal change (the difference in x-coordinates). A line with a steeper slope appears more inclined, while a line with a gentle slope seems less steep.
Parallel Lines: A Symphony of Equal Slopes
Now, let’s meet parallel lines, the lines that move in perfect unison. Parallel lines are like two dance partners, swaying in perfect harmony, never crossing paths. And what unites them? Their equal slopes. When two lines have the same slope, they remain eternally parallel, never intersecting. It’s like an invisible force keeping them on their separate paths.
Calculating Slope Using the Slope-Intercept Form
In the realm of geometry, understanding the slope of a line is crucial for various applications, including determining parallel lines. To calculate the slope, we delve into the ubiquitous slope-intercept form, represented as y = mx + b.
Imagine a line traversing the coordinate plane like a solitary traveler. The slope, denoted by m, quantifies the line’s inclination, or steepness. It reveals the ratio of vertical change (Δy) to horizontal change (Δx) as you embark on a journey along the line.
For instance, consider a line that ascends two units vertically for every three units it traverses horizontally. Its slope, m, would be 2/3. This ratio signifies that for every three steps you take to the right (Δx = 3), the line surges upward by two units (Δy = 2).
The slope-intercept form not only unveils the line’s steepness but also divulges its y-intercept, represented by b. This value indicates the line’s starting point on the y-axis, where it intersects the vertical axis.
By comprehending the slope and y-intercept, we gain insights into the line’s behavior and position within the coordinate plane. These parameters serve as invaluable tools for deciphering geometric relationships, paving the way for a deeper understanding of the intriguing world of lines.
Identifying Perpendicular Lines: Unraveling the Secret of Intersecting Lines
In the realm of geometry, lines intertwine in intricate ways, revealing relationships that govern their orientation and behavior. Perpendicular lines, a captivating class of intersections, stand out with their distinct 90-degree embrace.
What sets perpendicular lines apart is their ability to bisect each other, forming four congruent right angles. This special property stems from a mathematical connection that lies at the heart of their slopes.
The slope of a line, a measure of its steepness, holds the key to understanding perpendicularity. For perpendicular lines, the slopes are intimately linked by a unique relationship known as the negative reciprocal.
Consider two lines, l and m, that intersect perpendicularly. The slope of l, denoted by m_1, is the negative reciprocal of the slope of _m, denoted by m_2. In other words, _m_1 = -1/_m_2. This mathematical dance guarantees that the lines meet at a perfect 90-degree angle.
The negative reciprocal relationship between slopes provides a powerful tool for identifying perpendicular lines. If the slopes of two lines are negations of each other, then you can be confident that they will intersect perpendicularly, like two magnets drawn together with perfect alignment.
Understanding perpendicular lines is crucial in various fields, including architecture and construction. By ensuring that walls and other structures are perpendicular to each other, engineers and architects create sturdy and aesthetically pleasing designs.
Determining the Slope of a Line Parallel to a Given Line
In the realm of geometry, grasping the concept of slopes and parallel lines is essential. And when it comes to determining the slope of a line parallel to a given line, the notion of equality is key.
Parallel Lines: A Bond of Equal Slopes
Consider two lines that share a common characteristic: parallelism. What unites these lines is their identical slope. The slope, a measure of a line’s steepness, is the ratio of vertical change to horizontal change. When two lines are parallel, they maintain the same ratio of rise to run, ensuring their never-ending journey side by side.
Unraveling the Slope of a Parallel Line
To unravel the slope of a line parallel to a given line, we embark on a straightforward process:
-
Identify the slope of the given line: Determine the slope of the line that serves as our reference.
-
Embrace the Equality Principle: Once the slope of the given line is unveiled, we embrace the fact that the slope of our parallel line will echo this exact value.
-
Parallel Lines: Never Intersecting
With the slope of the parallel line firmly established, we arrive at a profound realization: these parallel lines will never cross paths. Their paths remain forever separate, never intersecting at any point on the coordinate plane. This unwavering parallelism symbolizes their constant, equidistant journey.
Parallel Lines in the Coordinate Plane: A Visual Exploration
Understanding Slope and Parallelism
Slope, a measure of a line’s steepness, is crucial in determining parallelism. Parallel lines share the same slope, meaning they never intersect.
Calculating Slope with the Slope-Intercept Form
The slope-intercept form (y = mx + b) provides a simple way to calculate slope. Slope (m) represents the ratio of vertical change to horizontal change along the line.
Example: Parallel Lines in the Cartesian Plane
Consider a line with the equation y = 2x + 3. Its slope is 2. To find the slope of a line parallel to it:
- Draw a Parallel Line: Draw a new line, parallel to the given line.
- Identify Slope: The new line shares the same slope, which is also 2.
- Equation of Parallel Line: Using the point-slope form, the equation of the parallel line can be written as y = 2x + b (where b is the y-intercept).
Non-Intersecting Parallel Lines
Parallel lines have the same slope, so their graphs are always parallel. They never intersect at any point, ensuring a constant vertical distance between them. This property makes them invaluable in various architectural and construction applications.
Understanding slope is essential for recognizing parallel lines. By mastering these concepts, you unlock the power to create and analyze parallel structures, whether in the abstract world of mathematics or the practical realm of real-world designs.