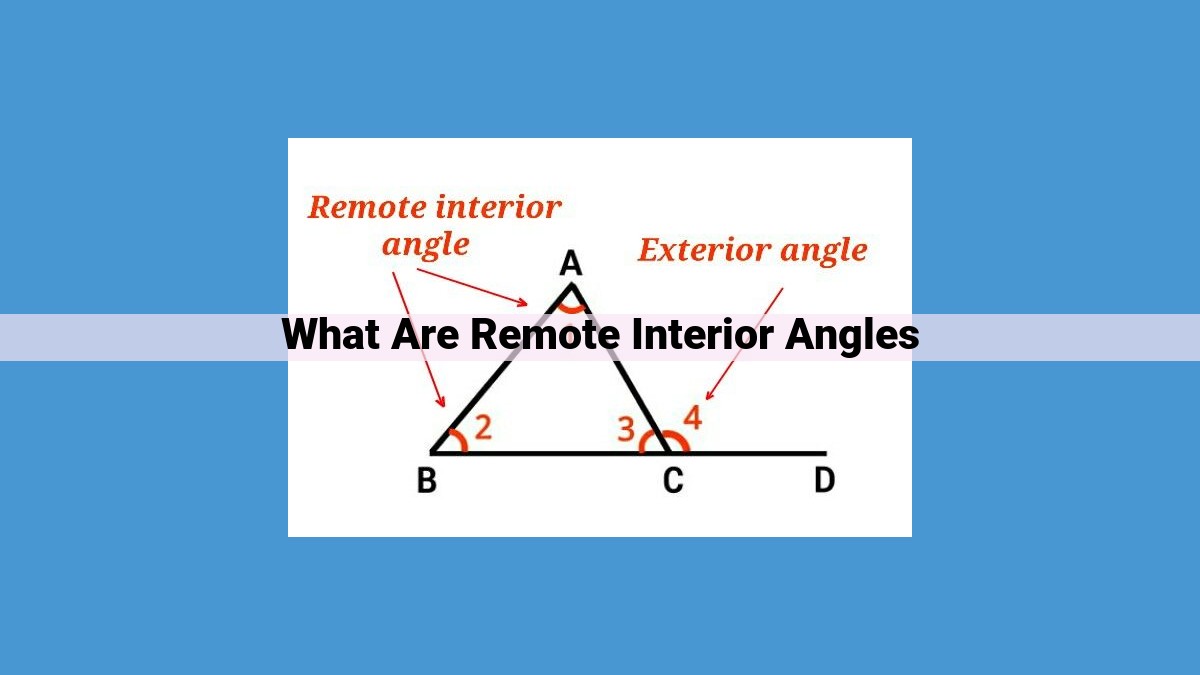
Remote interior angles are non-adjacent interior angles formed by two intersecting lines (transversals). They lie on opposite sides of the transversal and form a supplementary pair, measuring 180 degrees. Understanding remote interior angles is essential in geometry as they are directly related to the concept of corresponding angles and alternate interior angles, which are always congruent due to their position on the same side of the transversal.
Embarking on the Realm of Remote Interior Angles: Understanding Geometric Connections
In the realm of geometry, angles hold a pivotal role in defining shapes and relationships. Among the various types of angles, remote interior angles stand out with their significance. They emerge from the intersection of lines and transversals, bringing forth intriguing properties that unravel the essence of geometric configurations.
Defining Remote Interior Angles
When two lines intersect, they form four angles around the point of intersection. The interior angles are the two angles that lie on the same side of a transversal (a line that intersects both lines). Of these interior angles, the ones that do not share a common side are known as remote interior angles.
These remote angles play a crucial role in understanding geometric relationships. They provide insights into the congruence, supplementary nature, and relationships among various other angles, as we delve into their properties in the subsequent sections.
Understanding Interior Angles
In geometry, angles are a measure of the amount of rotation around a point. Interior angles are formed when two lines intersect. The angles that are created inside the intersection are called interior angles.
There are different types of interior angles, depending on their relationship to each other.
Adjacent Angles
Adjacent angles are two angles that share a common side and a common vertex. They are also known as consecutive angles. In the image below, ∠ABC and ∠BCD are adjacent angles.
[Image of adjacent angles]
Complementary Angles
Complementary angles are two angles that add up to 90 degrees. In the image below, ∠ABC and ∠ABD are complementary angles.
[Image of complementary angles]
Supplementary Angles
Supplementary angles are two angles that add up to 180 degrees. In the image below, ∠ABC and ∠CBD are supplementary angles.
[Image of supplementary angles]
Understanding interior angles is essential for solving many geometry problems. By understanding the different types of interior angles and their relationships to each other, you can solve problems involving angles with confidence.
Remote Interior Angles: A Geometrical Puzzle
In the realm of geometry, remote interior angles stand out as intriguing players that pique our curiosity. They’re not your typical interior angles. Instead, they’re angles that are separated by a transversal, a line that intersects two other lines.
Unlike adjacent interior angles, which share a common vertex and a side, remote interior angles are found on opposite sides of the transversal. Imagine two parallel lines intersected by a third line. The angles that lie on the inside of the parallel lines but on opposite sides of the transversal are remote interior angles.
These angles have a fascinating relationship with each other. In fact, they’re like two peas in a pod when it comes to measurement. They’re always supplementary, meaning they add up to 180 degrees. This is because they form a linear pair, a straight line.
The concept of remote interior angles is particularly important for solving geometric problems. Understanding their properties can help you navigate the intricacies of angle relationships, making geometry a breeze.
Related Angles: Alternate Interior and Corresponding Angles
In the fascinating realm of geometry, we encounter a special set of angles that hold a profound relationship with transversals. These angles, known as alternate interior angles and corresponding angles, play a pivotal role in understanding the intricate patterns formed when lines intersect.
Alternate Interior Angles
Imagine two parallel lines intersected by a transversal. The angles that lie on opposite sides of the transversal and inside the parallel lines are known as alternate interior angles. These angles are labeled as ∠1 and ∠3 or ∠2 and ∠4.
Corresponding Angles
Now, consider the angles that lie on the same side of the transversal and in corresponding positions relative to the parallel lines. These angles are called corresponding angles. For example, ∠1 and ∠5 or ∠2 and ∠6 are corresponding angles.
A Tale of Congruence
One of the most remarkable properties of alternate interior angles and corresponding angles is their congruence. This means that they have the same measure. This phenomenon arises from the positions of these angles in relation to the transversal.
In the case of alternate interior angles, the transversal forms a shared side between the angles. This shared side acts as a “mirror,” reflecting the angles on opposite sides. As a result, the angles become congruent.
Similarly, corresponding angles share a vertex and are formed by the intersection of the transversal and the same pair of parallel lines. This symmetrical arrangement ensures that the corresponding angles are also congruent.
The Significance of Congruence
The congruence of alternate interior angles and corresponding angles has far-reaching implications in geometry. It provides a powerful tool for proving theorems and solving problems involving parallel lines and transversals.
Furthermore, the concept of congruent angles is essential for understanding other geometric relationships, such as the properties of triangles and polygons. By comprehending the nature of alternate interior angles and corresponding angles, we unlock a deeper understanding of the intricate world of geometry.
The Supplementary Property of Remote Interior Angles: A Geometric Adventure
Embarking on a Geometric Quest
In the realm of geometry, there’s a captivating dance of angles and lines that governs the very essence of shapes. Among this geometric ensemble, remote interior angles stand out as enigmatic dancers, their movements defined by a peculiar supplementary property.
What are Remote Interior Angles?
Remote interior angles are a unique pair of angles that share a common vertex but do not share a side. They reside on opposite sides of a transversal that intersects two other lines. To visualize this, imagine a straight road (the transversal) crossing two parallel streets (the other lines). The angles formed where the transversal intersects each street are the remote interior angles.
The Supplementary Shuffle
Here comes the captivating twist: remote interior angles are always supplementary, meaning they add up to 180 degrees. It’s like a geometric ballet, where these angles gracefully align to form a perfect linear pair. This supplementary property arises from the nature of the transversal.
As the transversal intersects each line, it creates two pairs of adjacent angles (angles that share a common side). The remote interior angles are the non-adjacent angles within these adjacent pairs. It’s this arrangement that ensures their supplementary nature.
Linear Pairs: A Perfect Partnership
The supplementary property of remote interior angles has a close relationship with linear pairs. A linear pair is a pair of adjacent angles that add up to 180 degrees, forming a straight line. Therefore, remote interior angles, by being supplementary, necessarily form linear pairs.
The supplementary property of remote interior angles is a testament to the intricate interconnectedness of geometry. It highlights the interplay of lines and angles, revealing a harmonious balance within the geometric realm. Understanding this property unlocks a deeper appreciation for the beautiful dance of geometry.
Vertical Angles: Partners of Remote Interior Angles
Remote interior angles and vertical angles are two closely related angle pairs that play a significant role in geometry. Both types share a special connection through their position and shared vertex.
Remote interior angles are a pair of angles that lie on opposite sides of a transversal and outside the lines being crossed. Vertical angles, on the other hand, are two angles that form when two straight lines intersect. These angles are directly opposite each other, sharing the same vertex.
Adjacency and Congruence
Interestingly, remote interior angles are adjacent to vertical angles. This means they share a common vertex and a common arm. Additionally, vertical angles are always congruent, meaning they have the same measure. This property of vertical angles directly extends to remote interior angles.
Supplementary Connection
Another fascinating relationship between remote interior angles and vertical angles is that they are supplementary. This means that the sum of their measures is 180 degrees. This property is directly related to the fact that vertical angles are congruent. Since remote interior angles are adjacent to vertical angles, they are also supplementary, forming a straight line when the arms that define them are extended.
Linear Pairs
The supplementary relationship between remote interior angles and vertical angles also leads to the formation of linear pairs. A linear pair is a pair of adjacent angles that together measure 180 degrees. When remote interior angles are extended, they form a linear pair with the vertical angles to which they are adjacent.
Understanding the connection between remote interior angles and vertical angles is crucial for mastering geometry concepts. These angle pairs collaborate to form important geometric relationships, making them essential for solving various geometric problems. So, the next time you encounter these angles, remember their partnership and the supplementary bond they share.