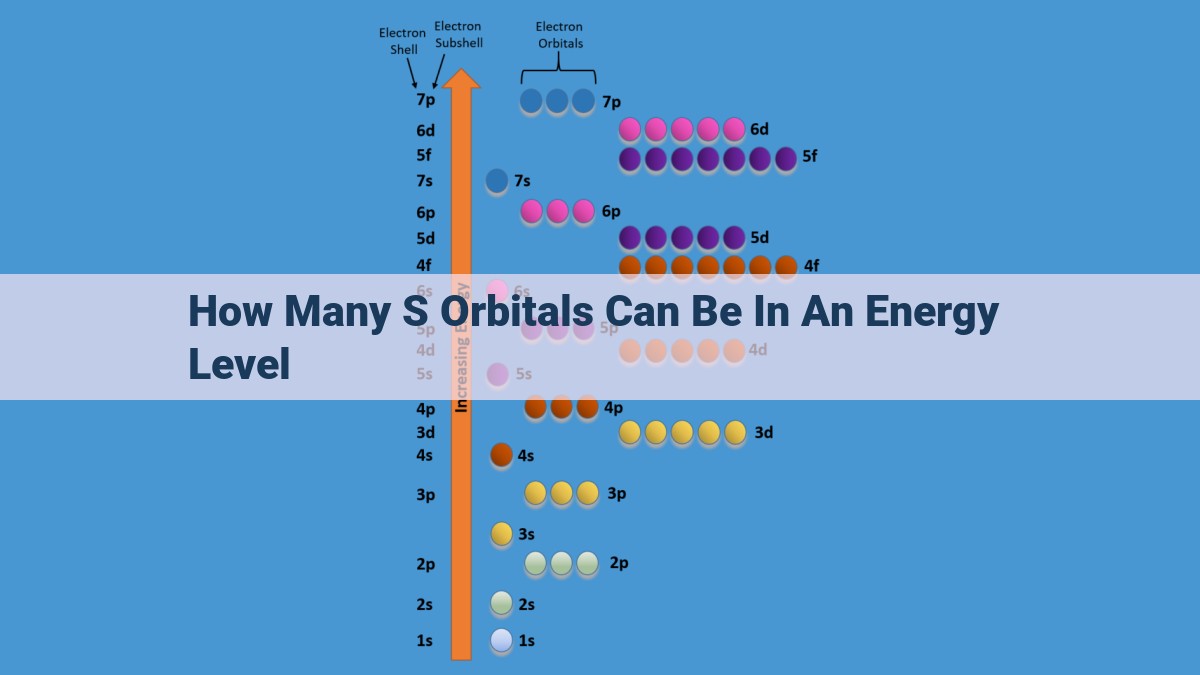
In an energy level, only one s orbital can exist, as dictated by the Pauli Exclusion Principle. This single s orbital has a spherical shape, with its wavefunction predicting the highest probability of finding electrons near the nucleus. The s orbital represents the lowest energy option within the energy level, and it is filled first according to the Aufbau Principle.
Delving into the Quantum Realm: Unveiling the Basics of Energy Levels and Quantum Numbers
In the atomic world, where the tiniest particles of matter reside, the distribution of electrons is governed by a set of principles known as quantum mechanics. These principles establish energy levels as discrete states in which electrons can exist. Each energy level is characterized by a specific quantum number, which describes the properties of an electron’s motion within that level.
One of the most important quantum numbers is the principal quantum number, or n, which designates the energy level’s distance from the atomic nucleus. The higher the value of n, the farther away the electron is from the nucleus and the higher its energy. Within each energy level, there are sublevels characterized by the angular momentum quantum number, or l. The value of l can range from 0 to n-1, and it determines the shape of the orbitals, the regions of space where electrons are most likely to be found.
Another crucial concept in quantum mechanics is the Pauli Exclusion Principle, which states that no two electrons in an atom can have the same set of quantum numbers. This principle ensures that each orbital can accommodate only two electrons, one with a spin of “up” and one with a spin of “down.”
Quantum Numbers: Unraveling the Secrets of Orbitals
Picture an electron, a tiny particle whirling around the nucleus, its dance choreographed by a set of rules known as quantum numbers. These numbers unveil the properties of orbitals, the regions where electrons dwell.
Principal Quantum Number (n):
The principal quantum number (n) denotes the energy level of an orbital. It’s like the floor of an apartment building, with higher numbers representing higher floors and thus higher energy levels.
Azimuthal Quantum Number (l):
The azimuthal quantum number (l) determines the orbital’s shape. It assigns letters to different shapes: s for spherical, p for dumbbell-like, and so on. The value of l indicates the nodal planes, regions where the electron wave function is zero.
Magnetic Quantum Number (ml):
The magnetic quantum number (ml) specifies the orientation of the orbital in space. Each value of l corresponds to multiple ml values, indicating different orientations. Think of it as the direction of a spinning top on a specific floor.
Spin Quantum Number (ms):
The spin quantum number (ms) describes the intrinsic spin of the electron. It can have two values, +1/2 or -1/2, representing two opposite spin directions. Each orbital can accommodate a maximum of two electrons with opposite spins, adhering to the Pauli Exclusion Principle.
The Pauli Exclusion Principle and Orbital Occupancy
Imagine a crowded nightclub, where it’s impossible for two people to occupy the same exact spot at the same time. This phenomenon, known as the Pauli Exclusion Principle, is also true in the realm of electrons. It dictates that no two electrons within an atom can have the exact same set of quantum numbers.
Quantum numbers are like unique identifiers that describe the properties of electrons, including their energy level, shape, and spin. According to the Pauli Exclusion Principle, electrons within the same atom must differ in at least one of their quantum numbers. This means that no two electrons can share the same orbital.
Orbitals are specific regions within an atom where electrons are most likely to be found. They are defined by their shape and energy level. The Pauli Exclusion Principle plays a crucial role in determining how electrons fill orbitals. It ensures that each orbital can only accommodate a maximum of two electrons, with opposite spins.
This restriction has profound implications for the distribution of electrons within an atom. Electrons tend to occupy the orbitals with the lowest energy levels first, filling up the s orbitals before moving on to the p orbitals, and so on. The Pauli Exclusion Principle ensures that electrons are evenly distributed throughout the available energy levels, contributing to the stability and chemical properties of elements.
Define an s orbital and describe its three-dimensional shape.
The Enigmatic s Orbital: Unveiling the Electron’s Spherical Haven
In the captivating world of quantum mechanics, electrons dance within specific regions known as orbitals. These ethereal spaces are characterized by unique energy levels and quantum numbers that define the electrons’ behavior. Among these orbitals, the s orbital stands out as a spherical haven, providing a cozy abode for a solitary electron.
Imagine the s orbital as a miniature sphere, its three-dimensional shape enveloping the nucleus like a protective bubble. Within this spherical realm, the electron moves freely, like a child playing in its own private playground. Its energy is at its lowest possible value for that energy level, ensuring the electron’s stability and contentment.
The electron’s behavior within the s orbital is governed by a mathematical function called a wavefunction. This function predicts the probability of finding the electron at any given point in space. Interestingly, the probability is highest at the nucleus, where the electron spends most of its time, like a faithful companion to its atomic core.
Unlocking the Secrets of the s Orbital: A Haven for Electron Behavior
Imagine an electron, like a tiny dancer, moving gracefully within a spherical space. This is the s orbital, a fundamental building block of any atom. But how does the electron know where to twirl and how it should behave? The answer lies in the wavefunction.
A wavefunction is a mathematical equation that describes the probability of finding an electron at any given point in space. For the s orbital, the wavefunction takes on a spherical shape, with its maximum value at the nucleus. This means that electrons are most likely to be found near the nucleus, but they can wander anywhere within the spherical boundary of the orbital.
The wavefunction is the electron’s blueprint, dictating its movements and guiding its behavior. It allows us to predict where the electron is likely to be at any moment, helping us understand the electronic structure of atoms and molecules.
Key Takeaway: The wavefunction of an s orbital is a spherical equation that reveals the probability of finding an electron at different points in space. It acts as a roadmap, guiding the electron’s dance within the orbital and providing insights into electron behavior.
The s Orbital: A Spherical Haven for Electrons
Meet the s orbital, the spherical haven where electrons love to cozy up. Picture a perfect ball, centered on the atom’s nucleus like a miniature planet. This three-dimensional abode welcomes electrons, allowing them to meander freely within its confines.
Imagine the nucleus as a glowing star, attracting the electrons like tiny magnets. The probability of finding an electron within the s orbital is highest at the nucleus’s doorstep, painting a vivid picture of electrons swarming around the nucleus like obedient satellites. As you venture further away from the nucleus, the probability of encountering an electron dwindles, until the electrons disperse into a sea of possibilities, distributed symmetrically around their spherical home.
Unraveling the S Orbital: A Lone Ranger in the Quantum World
In the realm of quantum physics, electrons dance within energy levels, each resembling a ladder with rungs representing quantum numbers. These numbers, like a celestial recipe, define the unique properties of electron orbitals, the regions where electrons roam. Among these orbitals, the s orbital stands out as a spherical haven, its electron residents enjoying a cozy, symmetrical abode.
The Solitaire Status of the S Orbital: One and Only
Unlike other orbitals, the s orbital exists as a solitary entity within each energy level. This exclusivity stems from a fundamental rule of electron occupancy, the Pauli Exclusion Principle. Imagine electrons as celestial dancers, each demanding their own stage. The Pauli Exclusion Principle ensures that no two electrons can share the same set of quantum numbers, effectively preventing multiple electrons from crowding into the same s orbital.
Electron Traffic and the S Orbital’s Priority
In the bustling metropolis of atoms, electrons obey a strict filling order, guided by the Aufbau Principle, their cosmic roadmap. This principle dictates that electrons first occupy orbitals with the lowest energy. And here, the s orbital shines as the frontrunner, boasting the lowest energy within each level.
Hund’s Rule and Electron Spin
As electrons settle into their orbitals, they face another choice: which direction to spin. This decision is governed by Hund’s Rule, which favors maximizing the number of unpaired electrons. In s orbitals, this rule manifests in electrons aligning their spins in the same direction, creating a harmonious ensemble.
The s orbital, a lone ranger in the quantum realm, plays a pivotal role in electron distribution. Its spherical shape, solitary nature, and priority in filling order make it a cornerstone of atomic structure. Understanding these concepts is essential for delving deeper into the intricate world of quantum mechanics and appreciating the elegance of nature’s design.
Explain how the Pauli Exclusion Principle prevents multiple electrons from occupying the same s orbital.
The Pauli Exclusion Principle: Nature’s Rule for Electron Cohabitation
In the bustling electron world, there’s an unspoken law that governs the behavior of these tiny particles: the Pauli Exclusion Principle. It’s like a strict chaperone at a social gathering, preventing electrons from getting too close and becoming overcrowded.
Imagine a quaint, spherical mansion known as the s orbital. It’s the electron’s cozy abode, a place where life is simple and wavefunctions dance like ballet. Now, envision two electrons trying to share this intimate space. According to the Pauli Exclusion Principle, this is a no-go zone.
Why the drama? Because electrons possess a whimsical, enigmatic attribute called spin. Think of it as their unique identity. And just like no two snowflakes are identical, no two electrons can have the same combination of energy level and spin within the same orbital.
So, picture this: one electron sets up camp in the s orbital, its spin pointing up like a proud peacock’s feather. Along comes another electron, eager to join the party. But wait! Nature throws up its hands and says, “Nope, not allowed!” The first electron’s spin orientation is already taken, so the second electron has no choice but to find another orbital to call home.
It’s as if the s orbital has become an exclusive club, with a strict “one electron, one spin” policy. This principle ensures that electrons maintain their individuality and play harmoniously within the atomic orchestra.
Delving into the Orbital Realm: Unraveling the Secrets of Electron Distribution
At the heart of every atom lies a bustling hub of electrons, each spinning and dancing within its designated space. To understand the intricate choreography of these subatomic particles, we embark on a journey into the realm of electron orbitals, starting with the fundamental concepts that govern their distribution.
Understanding the Quantum Landscape
Energy levels, akin to celestial tiers, define the allowed energy states electrons can inhabit. Quantum numbers, like celestial coordinates, describe the unique properties of each orbital. They reveal the electron’s energy level, shape, and orientation, much like the longitude, latitude, and altitude of a celestial body.
The Pauli Exclusion Principle emerges as a cosmic law, ensuring that no two electrons can occupy the exact same celestial abode. This principle shapes the very fabric of orbital occupancy, preventing electrons from crowding into the same energy level and spin state.
The s Orbital: A Spherical Haven
The s orbital stands apart as the cosmic cradle of electrons, assuming a spherical shape that envelops the nucleus like a protective aura. Its wavefunction, a mathematical veil that predicts electron behavior, portrays a symmetrical distribution of electrons throughout the sphere, with the highest probability of finding electrons at the nucleus, like celestial bodies orbiting a star.
The Solitary Status of the s Orbital
In the realm of orbitals, the s orbital reigns supreme as a celestial loner. Only one s orbital exists in each energy level, a testament to its unique structure. The Pauli Exclusion Principle acts as an orbital gatekeeper, preventing multiple electrons from squeezing into this spherical sanctuary.
Electron Traffic Regulation: Filling Order and the s Orbital’s Priority
As electrons embark on their celestial journey, the Aufbau Principle emerges as a guiding principle, dictating the order in which orbitals are filled. Like celestial traffic regulations, it ensures that electrons occupy the lowest energy orbitals first, much like cars filling into a parking lot. Hund’s Rule adds another layer of celestial etiquette, requiring electrons to align their spins parallel, akin to celestial bodies orbiting in harmony.
In this cosmic dance, the s orbital takes center stage, always filling first in each energy level. Its spherical symmetry grants it the lowest possible energy, making it the celestial equivalent of a prime parking spot. Thus, the s orbital serves as the foundational building block upon which the intricate symphony of electron distribution unfolds.
Describe Hund’s Rule and its role in determining the spin orientation of electrons.
Hund’s Rule: The Traffic Organizer for Electron Spin
Imagine electrons as tiny dancers, each with a unique spin like a whirling top. According to Hund’s Rule, these electron dancers prefer to keep their distance and avoid bumping into each other. This rule governs how electrons arrange their spins within orbitals, the designated spaces where they reside around the nucleus.
For a particular orbital, Hund’s Rule states that electrons initially fill the orbital with spins that are parallel to each other, like a group of hula hoopers spinning in the same direction. Only when the orbital is half-filled with parallel spins do electrons begin to pair up with opposite spins. This phenomenon is akin to a dance floor where couples only join hands once the solo dancers have taken their turn.
Hund’s Rule plays a crucial role in determining the stability and properties of atoms. By minimizing the repulsive forces between electrons with parallel spins, it ensures that electrons occupy the lowest energy configurations available. This rule is essential for understanding the electronic structure of atoms and molecules, which in turn influences their chemical behavior and properties.
Unlocking the Secrets of the Electron Highway: A Journey Through s Orbitals
In the realm of quantum mechanics, electrons dance around atomic nuclei in designated energy levels, each level comprising a series of orbitals. Among these orbitals, the s orbital stands out as a spherical haven for electrons, providing a cozy abode in the heart of the atom.
Meet the s Orbital: The Spherical Haven
Envision a sphere of probability, where electrons most likely reside at its center – that’s the s orbital. Its wavefunction, a mathematical description of an electron’s behavior, creates this three-dimensional spherical shape. This shape signifies that electrons in an s orbital are equally likely to be found in any direction from the nucleus.
Solitary by Nature: The Solitaire Status of the s Orbital
In each energy level, the s orbital exists as a lone wolf. The Pauli Exclusion Principle, a fundamental law of physics, prevents more than one electron from occupying the same exact state, thus ensuring the s orbital’s exclusivity.
The Hierarchy of Orbitals: Filling Order and the s Orbital’s Priority
As electrons fill orbitals, they follow the rules of the highway traffic: the Aufbau Principle and Hund’s Rule. The Aufbau Principle dictates that orbitals with the lowest energy get filled first. And guess what? The s orbital boasts the lowest energy, making it the first stop on the electron traffic route.
Hund’s Rule, on the other hand, governs the spin orientation of electrons. It states that electrons entering an orbital must have their spins aligned before they pair up with opposite spins. This ensures that orbitals are occupied with unpaired electrons as much as possible, minimizing the energy of the system.
The s orbital, with its spherical shape, solitary existence, and priority in filling order, plays a pivotal role in the electronic dance around the nucleus. Understanding this orbital’s unique properties is essential for unraveling the intricate architecture of atoms and the foundations of chemical bonding.