Slope embodies the concept of rate of change, unveiling how a quantity transforms over time or in relation to another variable. It finds expression as the derivative, gradient, velocity, or tangent, elucidating the trajectory of change. Whether in linear growth or curved trajectories, slope encapsulates the dynamic nature of change, enabling us to quantify and analyze patterns in various fields, including engineering, geography, and economics.
Unveiling the Essence of Slope: A Comprehensive Guide
In the tapestry of mathematics, the concept of slope emerges as a pivotal element, revealing the dynamic nature of change. It quantifies how a quantity transforms over time or in relation to another variable. Envision a winding road ascending a mountain; the slope represents the inclination of the road, indicating the rate at which you gain altitude with each stride.
Slope finds its expression in a myriad of forms: velocity, measuring the change in distance over time; gradient, describing the steepness of a slope; and differential, capturing the infinitesimal change of a function. At its core, slope embodies the rate of change.
Consider a thermometer measuring the temperature inside your home. As the sun rises, the temperature climbs steadily. The slope of the temperature-time graph reveals the velocity of this change, indicating how rapidly the temperature increases. Conversely, if you plunge a hot spoon into a cold beverage, the temperature declines swiftly, reflected in the negative slope of the temperature-time graph.
Slope is a polymorphic concept, manifesting in various guises. Gradient, a synonym for slope, highlights its diverse applications. In engineering, it determines the steepness of ramps and bridges; in geography, it governs the incline of hills and mountains; and in economics, it measures the rate at which prices change over time.
Delving deeper into the intricacies of slope, we encounter the tangent. It captures the dynamic essence of slope, representing the instantaneous rate of change of a curve at a specific point. Think of a speeding car; its tangent reveals its current velocity. In calculus and geometry, tangents play a pivotal role in understanding the behavior of curves and surfaces.
Linear growth epitomizes a special case of slope where the rate of change is constant. It manifests as a straight line on a graph, its slope indicating the proportional growth or uniform change of the quantity being measured.
Finally, the slope-intercept form provides a concise equation that encapsulates both the slope and the y-intercept of a straight line. This equation enables us to extract the slope directly, making it an invaluable tool for analyzing linear relationships.
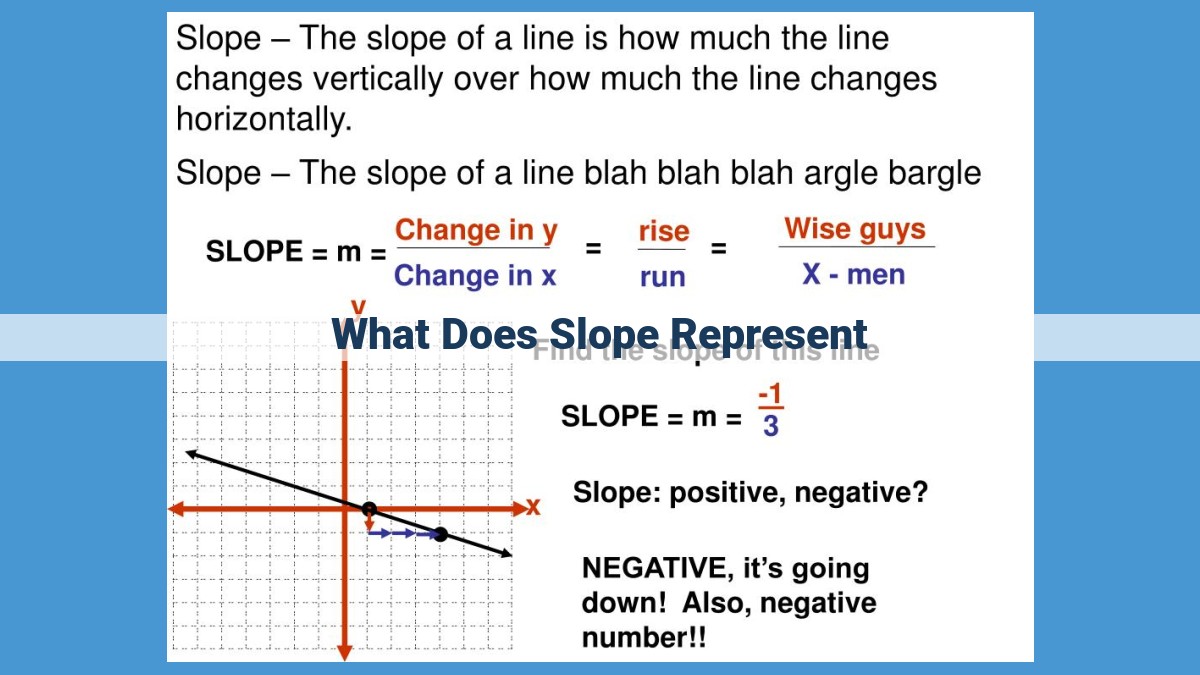
In practical contexts, the concept of rise over run emerges as an intuitive way to measure slope. It calculates the ratio of vertical change (rise) to horizontal change (run). This simple yet powerful tool finds applications in diverse fields, from architecture to surveying.
In conclusion, slope is a versatile concept that pervades multiple disciplines. It quantifies the rate of change, unveiling the dynamic nature of our world. From the ascent of a mountain to the rise of an economy, slope provides a fundamental understanding of how quantities transform over time or in relation to other variables. Embracing the power of slope empowers us to interpret and predict the ever-changing tapestry of our surroundings.
Slope: Unveiling the Fabric of Change
In the realm of mathematics, slope emerges as a pivotal concept, embodying the essence of rate of change. It measures the inclination of a line or curve, revealing how a quantity transforms over time or in relation to another variable.
Unveiling the Interwoven Trio: Slope, Velocity, and Gradient
Slope finds its kinship in the world of motion as velocity, capturing the rate at which an object traverses its path. Imagine a car accelerating along a highway; its velocity represents the slope of its distance-time graph. Delving into the terrain, the gradient of a hill echoes the slope, describing its steepness or inclination.
The Differential: A Calculus-Inspired Insight
Beyond the physical world, slope finds its counterpart in calculus as the differential. This mathematical tool measures the instantaneous rate of change of a function at a specific point. The differential epitomizes the infinitesimal shift in a function’s value as its input undergoes an infinitely small change.
Key Points for Enhanced Understanding:
- Slope serves as a ubiquitous measure of rate of change, appearing in diverse contexts from physics to economics.
- Velocity, gradient, and the differential are expressions of slope, capturing the essence of change in motion, terrain, and functions.
- Calculus unlocks the power of the differential, providing a precise tool to quantify the instantaneous rate of change.
Unveiling the Mathematical Essence of Slope: The Derivative
In our exploration of the enigmatic world of slope, we stumble upon its mathematical representation: the derivative of a function. Like a window into the dynamic nature of change, the derivative unveils the intricate relationship between how a quantity transforms over time or with respect to another variable.
Imagine a function, a curve that dances across the coordinate plane, embodying the ebb and flow of a particular quantity. The derivative, the mathematical wizard, analyzes this dance, capturing the instantaneous rate of change at each point along the curve. It’s like having a superpower, the ability to freeze time and measure the precise speed and direction of the function’s movement.
Mathematically, the derivative is represented as dy/dx, a cryptic symbol that holds immense power. dy represents the infinitesimally small change in the function’s output, while dx is the corresponding infinitesimally small change in the input. The quotient of dy/dx reveals the slope of the tangent line to the curve at that particular point, giving us an understanding of the function’s behavior in that specific instant.
This mathematical marvel is not merely an abstract concept; it has profound applications in fields ranging from engineering to economics. By harnessing the derivative, we can model the rate of flow in a pipe, predict the trajectory of a projectile, or analyze the fluctuations in stock prices. It empowers us to understand and quantify the dynamics of the world around us.
Gradient: Unveiling the Versatile Nature of Slope
In the realm of mathematics, the term “gradient” emerges as a synonym for the elusive slope, further accentuating its multifaceted guise. Slope, as we have explored, serves as a measure of change, a quantification of the rate at which a quantity evolves over time or with respect to some other variable. However, the gradient unveils a broader spectrum of its applications, transcending the confines of a single definition.
Gradient, a ubiquitous concept, manifests itself in a myriad of forms, each reflecting a unique perspective on the same underlying principle. Among its aliases, we encounter slope, an expression that embodies the steepness of a line; rate of change, capturing the essence of variation over time or space; incline, a term rooted in the physical world, describing the angle of ascent or descent; and pitch, a musical intonation, alluding to the gradient of sound waves.
The gradient finds its home not only in the classrooms of mathematics but also in the practical endeavors of engineering, where it governs the flow of liquids and the stability of structures. Geographers rely on gradients to地図surface elevations and delineate the contours of landscapes, while economists harness its power to understand the ebb and flow of markets.
Through its manifold manifestations, the gradient stands as a versatile tool, indispensable to a wide array of disciplines. By embracing its various forms, we gain a deeper appreciation for the multifaceted nature of slope and its pervasive influence on our world.
Understanding Slope: Exploring Its Many Guises
Slope, a fundamental concept in mathematics, unveils the dynamic nature of change, revealing how quantities evolve over time or with respect to other variables. This multifaceted concept finds expression in various interchangeable terms that paint a colorful tapestry of its applications.
-
Rate of change, measured as the variation in a quantity with time or distance, mirrors slope’s essence. Velocity, a tangible example of rate of change, describes an object’s speed and direction, while the gradient reflects the steepness of a slope. Physicists and engineers utilize the gradient as a benchmark for surfaces, signifying their angle of inclination.
-
Incline and pitch delve deeper into slope’s physical manifestations. Describing the gradient of a ramp or roof’s slant, these terms find their home in fields such as architecture and construction. Through these diverse expressions, slope’s versatility shines through, uniting diverse disciplines under its unifying banner.
What Slope Represents: Unveiling Its Versatility
In our everyday lives, we often encounter situations where quantities change over time or in relation to one another. From the velocity of a moving object to the incline of a hillside, slope plays a crucial role in capturing these changes. In this blog post, we’ll explore the multifaceted nature of slope, discovering its applications across diverse fields like engineering, geography, and economics.
Unveiling Gradient: Slope’s Synonymous Guise
Gradient is another commonly used term for slope, emphasizing its various forms. It encompasses concepts such as rate of change, incline, pitch, and slant. This range of terms reflects the wide-ranging contexts in which slope plays a pivotal role.
In engineering, gradients are crucial for designing structures and systems. For instance, the gradient of a ramp determines its steepness, which affects accessibility and safety. In geography, gradients are used to analyze topography and create elevation maps. The gradient of a river’s flow, for example, influences its erosive power and navigation feasibility.
Tangent: A Dynamic Perspective on Slope
Tangent refers to the slope of a curve at a specific point. It captures the momentary rate of change, providing a deeper understanding of dynamic systems. In calculus, tangents are used to analyze the behavior of functions and to find points of maximum and minimum values. In geometry, tangents are used to construct circles and ellipses, and to solve a variety of geometric problems.
Linear Growth: Embracing Constant Slopes
Linear growth occurs when the rate of change is constant. This is often represented by a straight line on a graph, with the slope of the line indicating the constant rate of change. In economics, linear growth models are used to describe steady economic growth or inflation. In population dynamics, linear growth models can be used to estimate the growth rate of a population over time.
Slope Intercept Form: Decoding the Slope
The slope intercept form of an equation is a special form that explicitly shows the slope of a straight line. This form is often used to write equations for lines, and to find the slope and intercepts of lines from their equations. In engineering and physics, slope intercept form is used to analyze linear relationships between variables, such as the relationship between voltage and current in an electrical circuit.
Rise Over Run: Measuring Slope in Practical Contexts
Rise over run is a simple yet powerful way to measure slope in practical contexts. It is the ratio of vertical change to horizontal change, and it can be used to calculate the slope of any straight line or inclined surface. In construction, rise over run is used to determine the slope of a roof or the angle of a staircase. In surveying, it is used to measure the slope of land or to create topographic maps.
Tangent: Unraveling the Dynamics of Slope
Embrace the Tangent: The Slope’s Guiding Force
Meet the tangent, the slope’s dynamic companion that captures the essence of change at a specific point on a curve. Just as a shadow follows you, the tangent trails a curve, providing a snapshot of its direction and steepness.
The Tangent’s Role in Unveiling Change
The tangent is a faithful companion to the slope, reflecting its rate of change. It tells us how rapidly a curve is ascending or descending at a particular instant. This knowledge empowers us to predict the curve’s future path.
Tangent’s Equation of Motion
Mathematically, the tangent is defined as the derivative of a function at a given point. The derivative measures the instantaneous rate of change and is the foundation of calculus, the language of change.
Tangent’s Applications: Unlocking Insights
Tangents hold great value in the world of calculus and geometry. They help us analyze the behavior of curves, understand the shape of surfaces, and solve complex problems. In engineering, they enable us to design optimal structures, while in economics, they aid in forecasting market trends.
The tangent is a powerful concept that sheds light on the dynamic nature of slope. By revealing the rate of change at specific points, it empowers us to understand and predict the behavior of curves. Its applications span diverse fields, providing invaluable insights into the world around us. So, next time you encounter a curve, embrace the tangent as your guide to unraveling its secrets.
Tangents: Unveiling the Significance of Tangents in Slope
Gather ’round, my fellow readers! Let’s delve into the fascinating world of tangents, where the secrets of slope lie. Tangents are like time-bending machines that capture the dynamic essence of slopes.
Imagine you’re on a roller coaster: as you zoom down the thrilling slopes, each point along your path represents a different slope. The tangent at each point tells you the instantaneous rate of change, the velocity of your ride. It’s like having a superpower to measure the steepness of the coaster at every moment!
Now, let’s break down the relationship between tangents and their slope-related buddies:
-
Slope: The rate of change of a function at a specific point. It tells you how the function is changing as you move along the curve.
-
Rate of Change: A more general term for slope, used to describe the change in any quantity over time or with respect to another variable.
-
Derivative: The mathematical representation of the rate of change, often calculated as the limit of the difference quotient.
-
Normal: A line perpendicular to the tangent at a given point, providing insight into the curvature of the function.
Together, these concepts paint a vibrant picture of the dynamic nature of slopes. Just like a tangent captures the instantaneous velocity of a roller coaster, it also reveals the slope, rate of change, derivative, and normal that define the curve at that moment.
So, there you have it, folks! Tangents are the unveilers of slope’s secrets, giving us a deeper understanding of the changing landscape of functions. Stay tuned for more slope adventures in our next blog post!
The Tangent’s Tale: Unraveling Curves and Surfaces
In the realm of calculus and geometry, the tangent plays a pivotal role, unveiling the secrets hidden within curves and surfaces. Like a guiding light, it illuminates the path of change, guiding us toward a deeper understanding of these intricate shapes.
Imagine a roller coaster winding its way through the amusement park. The constant up and down of the track can be described by a curve. At any given moment, the slope of the tangent to the curve represents the instantaneous rate of change of the roller coaster’s height as it hurtles along the track.
Similarly, the tangent has a profound impact in the study of surfaces. Think of a gently sloping hillside, its contours traced by a multitude of curves. The gradient vector of each point on the surface, perpendicular to the tangent, points in the direction of the steepest descent. This knowledge is crucial in fields such as hydrology and architecture, where understanding water flow and designing structures that withstand gravity’s pull are essential.
The tangent’s power extends beyond the realm of curves and surfaces. In the intricate world of differential equations, it serves as a guide, pointing toward solutions that describe the behavior of complex systems. It’s a tool that unlocks the hidden relationships within our mathematical universe, revealing the patterns and symmetries that shape our understanding of the world around us.
So, as we delve into the realm of calculus and geometry, let us embrace the tangent, not merely as a mathematical concept, but as a guiding force that empowers us to unravel the complexities of curves and surfaces, illuminating the hidden beauty and order that lies beneath.
Linear Growth: The Constant Climbing Rate
Imagine a budding entrepreneur who launched their business with a modest investment. As their venture gains traction, its revenue grows at a steady pace, month after month. This unwavering growth pattern is an example of linear growth, where the rate of change remains constant.
Unlike exponential growth, where the rate of change accelerates over time, linear growth progresses at a consistent pace. This means that for every equal increment of time, there is a corresponding equal increment in the dependent variable. In our entrepreneur’s case, for every additional month of operation, the revenue increases by a fixed amount.
Graphically, linear growth is represented by a straight line with a constant slope. The slope of a line is the measure of its steepness and is calculated as the ratio of the vertical change (rise) to the horizontal change (run). In the case of linear growth, the constant slope indicates that the rate of change is unwavering.
Linear growth is ubiquitous in nature, from the gradual rise of a sourdough bread in the oven to the steady increase in the value of a long-term investment. Understanding linear growth empowers us to make informed predictions about future outcomes. By recognizing the constant rate of change, we can extrapolate the trend to estimate future values.
Linear growth is a cornerstone of financial planning, economic modeling, and scientific research. Its simplicity and predictability make it a valuable tool for forecasting, budgeting, and understanding real-world phenomena. So, the next time you encounter a steadily increasing trend, remember the concept of linear growth: a constant climbing rate that shapes the predictable progression of countless systems.
What Slope Represents: Unveiling Its Multifaceted Nature
Slope, a ubiquitous concept in mathematics, plays a crucial role in our understanding of the world around us. It is a measure of how a quantity changes with respect to another, offering insights into patterns and trends that might not be immediately apparent.
1. Rate of Change: Unleashing the Power of Slope
Slope represents the rate of change—the pace at which a quantity varies over time or with respect to another variable. Think of it as the speedometer of a car, indicating how fast the car’s distance from the starting point is increasing. Velocity, gradient, and differential are all terms used interchangeably to describe this fundamental concept.
2. Linear Growth: Embracing Constant Slopes
In a special scenario known as linear growth, the rate of change remains steady. This means that the quantity increases or decreases at a constant pace, like a car traveling at a set speed. Linear growth is often described as proportional growth or uniform change.
3. Slope Intercept Form: Unraveling the Equation of Growth
The slope intercept form of a linear equation explicitly reveals the slope. It is a convenient way to represent a straight line, providing both the slope and the y-intercept (the point where the line crosses the y-axis). By calculating the slope from the slope intercept form, we can determine the rate of change directly.
4. Rise Over Run: A Practical Perspective on Slope
In practical terms, slope can be measured using the rise over run formula. By dividing the vertical change“ (rise) by the horizontal change (run), we obtain the slope. This approach is particularly useful in situations like determining the steepness of a hill or the gradient of a river.
Understanding the Concept of Slope: A Journey of Rate of Change and Tangents
In the realm of mathematics, slope emerges as a fundamental concept that unveils the rate of change of a quantity. It embodies the notion of how a variable transforms with respect to another, like a dancer’s graceful movements. To grasp the essence of slope, let’s embark on an enlightening journey through its various manifestations.
Unveiling the Gradient: A Multifaceted Expression of Slope
The gradient and slope are synonymous terms, like two sides of the same coin. They represent the rate of change, revealing how a quantity ascends or descends. Imagine a winding mountain road, where the gradient, like a faithful guide, indicates its steepness. It’s not just limited to geography; gradient finds its place in engineering, economics, and beyond, guiding us through complex data landscapes.
Capturing the Dynamic Nature of Slope with Tangents
At any given point on a curve, the tangent captures the slope’s dynamic nature. It’s like a snapshot of the slope at that precise instant, telling us the instantaneous rate of change. Just as a tangent line touches a curve at a single point, so too does the tangent slope provide a localized insight into a function’s behavior.
Embracing the Simplicity of Linear Growth: Constant Slopes
When a quantity changes at a steady pace, we encounter linear growth. Think of a car driving at a constant speed, its rate of change remaining ever faithful. Linear growth manifests itself graphically as a straight line, its slope holding the key to the rate of change.
Decoding the Equation: Slope Intercept Form Reveals the Slope’s Secrets
The slope intercept form of a linear equation unveils the slope’s hidden message. Like a coded transmission, it reveals the slope explicitly, accompanied by the y-intercept, a crucial datum. By deciphering this equation, we gain insight into the line’s behavior, much like a detective solving a mathematical puzzle.
Rise Over Run: A Practical Measure of Slope
In the world beyond equations, rise over run provides a tangible way to measure slope. Imagine a hiker scaling a mountain, their vertical ascent (rise) relative to their horizontal progress (run) determines the slope of their arduous journey. This same concept finds applications in diverse fields, from construction to navigation, helping us navigate the slopes of our physical environment.
Define slope intercept form as the equation of a straight line that explicitly shows the slope.
Slope Intercept Form: Unlocking the Secret of a Straight Line’s Slope
In the realm of mathematics, the slope intercept form is a magical equation that holds the key to understanding the slope of a straight line. It’s like a decoder ring that reveals the line’s rate of change, or how steeply it’s climbing or falling.
The slope intercept form is a special type of linear equation that looks like this:
y = mx + b
where:
- y is the dependent variable (what’s changing)
- x is the independent variable (what’s causing the change)
- m is the slope
- b is the y-intercept (where the line crosses the y-axis)
The slope is a mysterious number that tells us how fast y changes as x increases. It’s the ratio of the rise (vertical change) to the run (horizontal change) of the line. If the slope is positive, the line is going uphill as you move from left to right. If it’s negative, the line is going downhill.
The y-intercept is where the line crosses the y-axis. It tells us the value of y when x is equal to zero.
To find the slope of a straight line using the slope intercept form, simply look at the coefficient of x, which is the number in front of x. That number is the slope!
The slope intercept form is a powerful tool that allows us to understand and analyze straight lines. It helps us visualize how the line is changing, find its equation, and even predict future values of y for any given value of x.
So, if you want to unravel the secrets of a straight line’s slope, remember the slope intercept form:
y = mx + b
Where m is the slope and b is the y-intercept. With this equation, you’ll be a geometry master, ready to conquer any slope that comes your way.
What Slope Represents: Unveiling the Language of Change and Growth
In the world of mathematics, slope is a concept that unravels the secrets of change and growth. It’s like a roadmap that guides us through the intricate landscapes of functions, graphs, and real-world phenomena.
Slope as Rate of Change
Just as velocity measures the rate of change in an object’s position, slope measures the rate of change in a function or variable over another. It tells us how much a quantity is increasing or decreasing with respect to another quantity.
Gradient: Slope in Disguise
Gradient and slope are interchangeable terms. It’s like having different aliases for the same secret agent. The term “gradient” is often used in fields like engineering, geography, and economics to describe the steepness of a slope or the rate of change in a physical or economic system.
Tangent: The Dynamic Duo of Slope
Imagine a tangent as a line that touches a curve at a single point. Its slope at that point is like a snapshot of the curve’s rate of change at that instant. Tangents are essential tools in calculus and geometry for understanding the behavior of curves and surfaces.
Linear Growth: Constant Slope
When the rate of change is constant, we have linear growth. It’s like a steady climb or descent where the slope remains the same. Linear growth can be represented by a straight line on a graph, with the slope as its constant steepness.
Slope Intercept Form: Unlocking the Slope’s Secret
The slope intercept form of a linear equation is like a code that reveals the slope. It’s an equation that explicitly shows the slope as the coefficient of the x variable. By decoding this form, we can easily extract the slope and understand the linear behavior of the function.
Rise Over Run: Slope in the Real World
In practical settings, slope can be measured using the rise over run ratio – the vertical change divided by the horizontal change. This ratio is equivalent to slope, gradient, and rate of change, and it’s often used in areas like architecture, engineering, and everyday life to measure slopes and inclinations.
Slope is a versatile chameleon, changing its guise and terminology depending on the context. But it always retains its fundamental role as the measure of rate of change, helping us navigate the dynamic world of mathematics and beyond.
Unraveling the Mystery of Slope: A Comprehensive Guide
Slope, a mathematical concept that permeates various disciplines, offers insights into how quantities change over time or with respect to other variables. This article serves as a comprehensive guide to understanding slope, exploring its various forms and applications.
Rate of Change: Unveiling Slope’s Core Nature
Slope is fundamentally a measure of rate of change, quantifying how a quantity changes over time or with respect to an independent variable. It is expressed as the ratio of vertical change (rise) to horizontal change (run). Think of it as the gradient of a line, indicating its steepness or direction.
Tangent: Capturing the Dynamic Nature of Slope
At any given point on a curve, the slope can be determined using its tangent, a straight line that touches the curve at that point. The slope of the tangent line represents the instantaneous rate of change of the curve at that point.
Linear Growth: Embracing Constant Slopes
In linear growth, the rate of change is constant, resulting in a straight line on a graph. This constant slope reflects the uniform change in the dependent variable (y) with respect to the independent variable (x).
Slope Intercept Form: Decoding the Equation that Embodies Slope
The slope intercept form of a linear equation, y = mx + c, explicitly expresses the slope (m). It represents the rise over run of the line, where ‘m’ is the change in y per unit change in x and ‘c’ is the y-intercept.
Rise Over Run: Measuring Slope in Practical Contexts
The rise over run method provides a straightforward way to measure slope in real-world applications. It involves identifying the vertical change (rise) and horizontal change (run) between two points on a line. This ratio represents the slope, allowing us to quantify the steepness or slant of terrain, roadways, or any other linear feature.
Unveiling the True Essence of Slope
In everyday life, we often encounter slopes without realizing their significance. From the gentle incline of a hill to the steep ascent of a mountain, slopes are all around us. But what exactly defines slope and how does it impact different scenarios? Let’s embark on a storytelling journey to uncover the multifaceted nature of slope.
Rise Over Run: The Essence of Slope
Imagine a hiker traversing a rugged mountain trail. As he ascends, he covers not only horizontal distance but also vertical elevation. The rise is the amount of vertical height he gains, while the run is the horizontal distance he travels. The rise over run ratio, expressed as slope, quantifies the steepness of the trail.
Key takeaway: Slope is a measure of the steepness of a line or surface, calculated as the ratio of vertical change (rise) to horizontal change (run).
Gradient and Its Guises
Slope is often referred to as gradient, which essentially means the same thing. But don’t be fooled by different terms! Incline and pitch are other expressions of gradient, each emphasizing the angle of a slope. Engineers use gradient to design roads and buildings, geographers to describe terrain, and economists to analyze market trends.
Tangent: Connecting Slope and Curvature
When we deal with curved lines, the concept of slope becomes more dynamic. The tangent to a curve at a specific point represents the slope of the curve at that point. It’s like a snapshot of the curve’s steepness at a particular instant. Tangents are crucial in calculus and geometry, helping us understand the behavior of curves and surfaces.
Linear Growth: Embracing Constant Slopes
In some situations, the rate of change remains constant over time. This is known as linear growth, where the slope of the graph is a constant value. Linear growth is often seen in processes like population increase, bacterial growth, and chemical reactions.
Slope Intercept Form: Deciphering the Equation
The slope intercept form of a linear equation (y = mx + b) provides us with a direct representation of the slope (m). The slope intercept form is used extensively in graphing, data analysis, and solving algebraic problems.
Rise Over Run: Measuring Slope in the Real World
Rise over run is a versatile concept that finds applications in various fields. Hikers use it to assess trail difficulty, architects to design ramps, and pilots to calculate flight paths. By understanding the rise over run ratio, we can make informed decisions in real-world situations.
In conclusion, slope is a fundamental concept that plays a vital role in understanding the rate of change, the steepness of surfaces, and the behavior of curves. Whether you’re hiking a mountain, designing a building, or analyzing data, grasping the essence of slope will empower you to navigate the challenges and unravel the mysteries of the world around you.
Rise Over Run: Unraveling the Equivalence of Slope, Gradient, and Slant
In our exploration of the multifaceted concept of slope, we encounter a crucial aspect that unites several seemingly distinct terms: rise over run. This ratio, expressing the change in vertical distance relative to the change in horizontal distance, serves as a cornerstone for understanding how slope, gradient, rate of change, and slant are intimately connected.
Gradient: A Synonym for Slope, Unveiling Its Varied Forms
Gradient, often synonymous with slope, captures the inclination or steepness of a surface or curve. Whether discussing the slope of a hill, the gradient of a temperature change, or the inclination of a roof, this term encompasses the rate at which a quantity changes across a given distance.
Rate of Change: Unveiling the Dynamic Nature of Slope
Rate of change lies at the heart of understanding slope. It measures how a quantity varies with respect to another variable. The slope of a line, for instance, represents the rate at which the y-coordinate changes for a given change in the x-coordinate. This rate can be positive, negative, or zero, reflecting the direction and magnitude of change.
Slant: A Layman’s Term for Slope, Embracing Real-World Applications
Slant, a more colloquial term for slope, is commonly used in everyday conversations to describe the inclination of surfaces. We might say that a roof has a steep slant or that a road has a slight slant. These informal expressions convey the same concept as slope, capturing the angle or inclination of an object or terrain.
Rise Over Run: The Common Thread Unifying These Terms
The concept of rise over run provides a unifying framework for these seemingly diverse terms. It defines slope as the ratio of the vertical change (rise) to the horizontal change (run). This ratio captures the gradient, rate of change, or slant of a line, surface, or curve.
Practical Applications: Embracing the Versatility of Rise Over Run
The concept of rise over run finds practical applications in numerous fields, including engineering, geography, and architecture. Engineers use it to calculate the slope of roads and buildings, ensuring structural stability and accessibility. Geographers employ it to map the topography of landforms, understanding the flow of water and erosion patterns. Architects rely on it to design sloped roofs and ramps, balancing aesthetics and functionality.
Through the lens of rise over run, we unravel the equivalence between slope, gradient, rate of change, and slant. These seemingly distinct terms converge to capture the inclination or rate of change in various contexts. Whether exploring the slope of a mountain, the gradient of a curve, or the slant of a roof, this unifying concept provides a common language for describing and understanding the dynamic nature of these phenomena.
Rise Over Run: Measuring Slope in Practical Contexts
Let’s imagine you’re hiking up a steep mountain trail. As you climb, you may notice that the slope of the trail becomes steeper. This slope represents the rate of change in your elevation as you progress along the trail.
In practical terms, rise over run is a simple way to measure this slope. Rise refers to the vertical change, while run refers to the horizontal change. By dividing the rise by the run, you can calculate the gradient, which is another term for slope.
For instance, if you hike 200 feet vertically (rise) and cover 500 feet horizontally (run), your slope would be 200/500 = 0.4. This means that for every foot you travel horizontally, you gain 0.4 feet in elevation.
Rise over run is used in a wide range of fields, including:
- Engineering: To design slopes for roads, bridges, and other structures that are safe and efficient.
- Geography: To measure the slope of terrain for mapping and land-use planning.
- Economics: To analyze changes in prices or other economic indicators over time.
By understanding rise over run, you can better appreciate the rate of change in many different real-world situations.