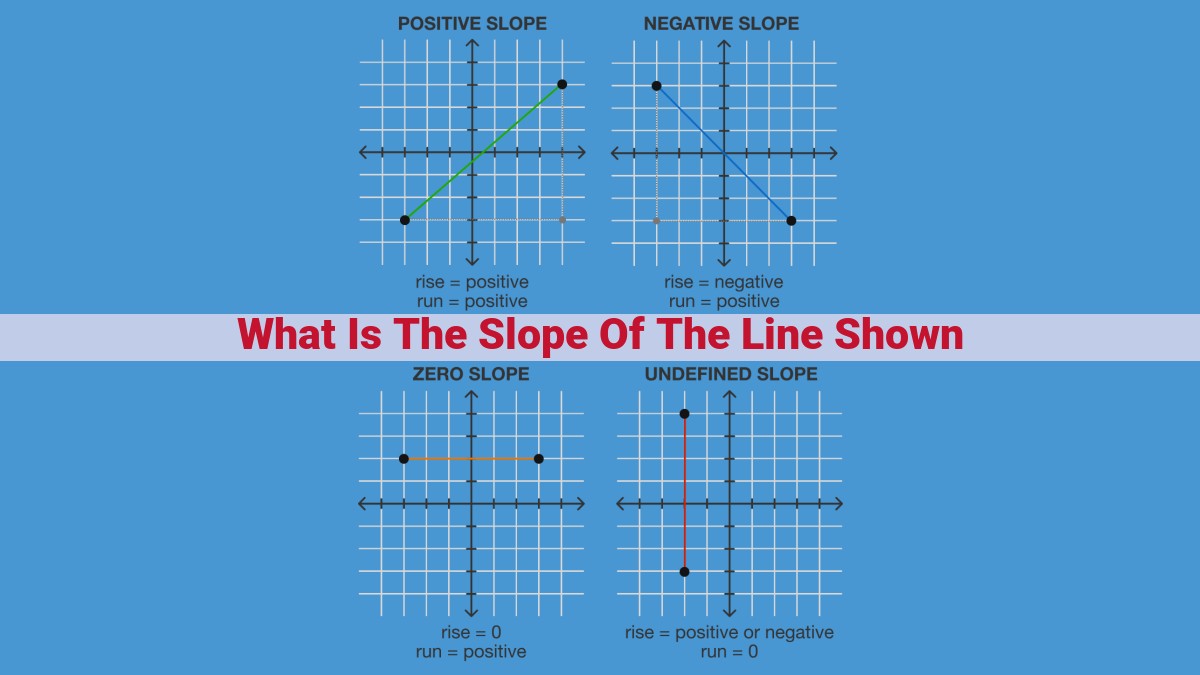
Slope reflects a line’s steepness, quantifying its vertical change (rise) relative to its horizontal change (run). Positive slopes indicate upward movement, negative slopes downward movement, zero slopes flat lines, and infinite slopes vertical lines. The slope formula, Slope = (y2 – y1) / (x2 – x1), calculates the slope using two points (x1, y1) and (x2, y2). Slope finds applications in diverse fields, from architecture (building slopes) to physics (projectile motion) and economics (supply and demand curves), showcasing its importance in understanding and analyzing real-world phenomena.
Understanding Slope:
- Explain the concept of slope as the measurement of a line’s steepness.
- Define the terms “vertical change” and “horizontal change” and their significance in understanding slope.
Understanding the Language of Lines: Exploring the Concept of Slope
In the world of geometry, lines hold a special significance. They can guide us, separate spaces, and even express emotions. One key aspect of understanding lines is grasping the concept of slope, a measure that reveals the line’s “inclination” or steepness.
Slope is essentially the ratio between the vertical change (the change in y-coordinates) and the horizontal change (the change in x-coordinates) of any two points on the line. This ratio provides insight into the angle at which the line ascends, descends, or remains flat.
Imagine a hill climbing upwards; its positive slope represents the line’s inclination in the upward direction. Conversely, a hill sloping downwards exhibits a negative slope, indicating a downward movement. A horizontal line, parallel to the x-axis, has a zero slope, as there is no vertical change. Lastly, a vertical line, parallel to the y-axis, boasts an infinite slope, signifying an undefined ratio.
Understanding the Language of Lines: The Concept of Gradients
Have you ever wondered how architects design sloping rooftops or engineers calculate the stability of bridges? The secret lies in understanding the concept of gradients, also known as slopes. They describe the steepness and direction of lines, playing a crucial role in various fields.
Types of Gradients: A Spectrum of Slopes
Positive Gradients:
Imagine a line that rises from left to right. This line has a positive gradient, indicating that it slants upward. The greater the rise (vertical change) compared to the run (horizontal change), the steeper the incline.
Negative Gradients:
In contrast, a line that falls from left to right has a negative gradient. As you move along this line, you descend, creating a downward slope. The steeper the decline, the greater the drop in vertical change relative to horizontal change.
Zero Gradients:
Horizontal lines, which run parallel to the x-axis, have a zero gradient. They represent no slope or change in direction.
Infinite Gradients:
Vertical lines, extending straight up or down, have an infinite gradient. Their vertical change is undefined in relation to horizontal change, creating a steep and abrupt rise or fall.
Illustrating the Spectrum
- Positive Gradient: A line with a positive gradient (e.g., y = 2x + 1) rises upward, as seen in the roof of a house.
- Negative Gradient: A line with a negative gradient (e.g., y = -x + 3) slopes downward, representing the declination of a hill.
- Zero Gradient: A line with a zero gradient (e.g., y = 5) remains horizontal, like a flat road.
- Infinite Gradient: A line with an infinite gradient (e.g., x = 10) runs vertically, such as the side of a staircase.
Remember, gradients are not limited to mathematics. They have practical applications in architecture, engineering, physics, and economics, helping us describe the world around us and solve complex problems.
Calculating the Slope: A Step-by-Step Guide
In our journey through the fascinating world of geometry, we encounter lines with varying steepnesses, a characteristic known as slope. Understanding slope empowers us to decipher the hidden patterns in the world around us, from analyzing economic trends to designing incredible structures.
To embark on this adventure, let’s unravel the secret formula for calculating slope: Slope = (y2 – y1) / (x2 – x1). Allow us to break down this equation into digestible terms:
-
y2 – y1: This represents the vertical change, which is the difference between two points on the line’s y-axis.
-
x2 – x1: This represents the horizontal change, which is the difference between two points on the line’s x-axis.
Equipped with this formula, we can now determine the slope of a line with ease. Simply follow these steps:
-
Identify Two Points: Choose any two points (x1, y1) and (x2, y2) that lie on the line.
-
Calculate Vertical Change: Compute the difference between the y-coordinates of the two points: y2 – y1.
-
Calculate Horizontal Change: Similarly, find the difference between the x-coordinates of the two points: x2 – x1.
-
Divide Vertical Change by Horizontal Change: Using the formula, divide the vertical change by the horizontal change: (y2 – y1) / (x2 – x1).
The result of this calculation is the slope of the line. A positive slope indicates a line that rises from left to right, a negative slope indicates a line that descends from left to right, a zero slope indicates a horizontal line, and an infinite slope indicates a vertical line.
Mastering the art of calculating slope unlocks a multitude of practical applications in various fields:
-
Architecture: Architects use slope to design buildings and roads that are both functional and aesthetically pleasing.
-
Engineering: Engineers rely on slope to create structures that can withstand forces and maintain stability.
-
Physics: Physicists use slope to analyze projectile motion, helping us understand the trajectories of objects in motion.
-
Economics: Economists use slope to analyze supply and demand curves, enabling them to make informed predictions about market behavior.
So, let us embrace the power of slope and unlock the hidden secrets of the world!
Understanding Slope: A Foundation for Exploring Various Fields
In the realm of mathematics, slope holds a pivotal role in quantifying the steepness or inclination of a line. From the gentle curves in architecture to the intricate designs of engineering marvels, from the trajectories of projectiles to the fluctuations of economic trends, slope plays a crucial part in shaping our world. Embark on an enlightening journey as we delve into the captivating applications of slope across diverse fields, unraveling its remarkable significance.
Architecture: Crafting Slopes that Shape Our Built Environment
Slope serves as the cornerstone for designing functional and aesthetically pleasing architectural structures. Architects meticulously calculate the slope of building slopes and roads, ensuring safe and efficient movement for pedestrians and vehicles alike. By manipulating the slope, they create ramps, staircases, and even skyscrapers that seamlessly connect spaces and enhance the overall user experience.
Engineering: Designing Structures that Withstand Nature’s Forces
In the realm of engineering, slope is an indispensable metric for ensuring structural integrity. Engineers rely on slope to design bridges, buildings, and other structures that can withstand the relentless forces of nature, such as earthquakes and high winds. By carefully calculating the slope of various components, they create resilient infrastructure that protects lives and property.
Physics: Unraveling the Secrets of Projectile Motion
Slope plays a fundamental role in understanding projectile motion, a phenomenon that governs the trajectory of objects launched into the air. The angle of the launch, known as the angle of projection, directly influences the slope of the projectile’s path. By analyzing the slope, physicists can predict the distance traveled and the height reached by the projectile, offering valuable insights into the behavior of objects in motion.
Economics: Analyzing Market Dynamics with Slope
In the ever-changing landscape of economics, slope is a vital tool for analyzing market trends. By studying the slope of supply and demand curves, economists gain valuable insights into the relationship between price and quantity demanded. The steeper the slope, the more responsive consumers are to changes in price, providing valuable information for businesses and policymakers alike.
Mastering the concept of slope is not merely an academic pursuit but an essential key to unlocking the mysteries of various fields. From the structural integrity of buildings to the intricacies of projectile motion, from the design of highways to the dynamics of economic markets, slope permeates every aspect of our world, shaping its form and function. By embracing the power of slope, we empower ourselves to create a better, more informed, and more connected world.