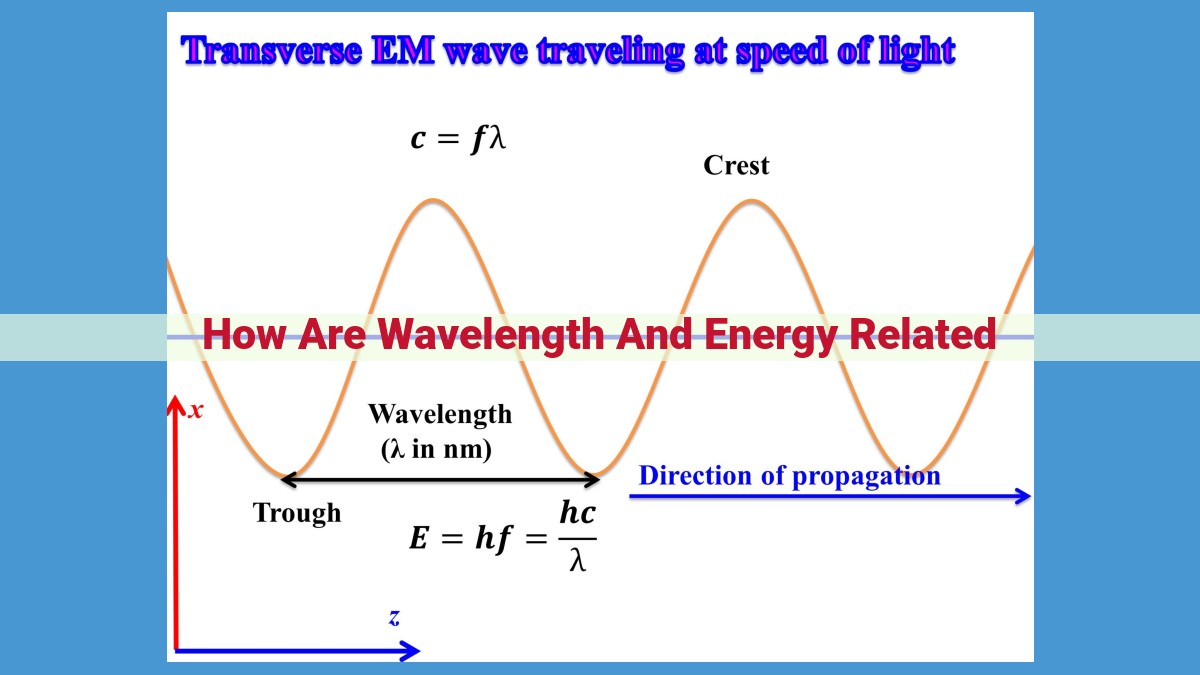
Wavelength and energy in electromagnetic radiation are inversely related. As wavelength increases, energy decreases, while shorter wavelengths indicate higher energy. This relationship, described by Planck’s constant, is E = hν, where E represents energy, h is Planck’s constant, and ν is frequency. Higher frequencies correspond to shorter wavelengths and higher energy, while lower frequencies correspond to longer wavelengths and lower energy. This inverse relationship forms the basis of the electromagnetic spectrum, with radio waves having the longest wavelengths and lowest energy, and gamma rays having the shortest wavelengths and highest energy.
Inverse Relationship: Understanding the Connection Between Energy, Frequency, and Wavelength
- Describe the inverse relationship between wavelength, energy, and frequency.
- Explain that as wavelength increases, energy and frequency decrease, and vice versa.
Inverse Relationship: Unveiling the Connection Between Energy, Frequency, and Wavelength
In the vast realm of physics, there exists an intriguing dance between three fundamental properties: energy, frequency, and wavelength. These properties are inextricably linked, forming an inverse relationship that governs the behavior of electromagnetic radiation.
Imagine a rhythmic wave undulating through space. Wavelength refers to the distance between two consecutive crests or troughs of this wave. As the wavelength increases, both energy and frequency decrease. Conversely, when the wavelength shortens, energy and frequency rise. This inverse relationship is a cornerstone of understanding the behavior of light and other forms of electromagnetic radiation.
Consider the concept of energy as the capacity to perform work. Higher energy corresponds to shorter wavelengths and higher frequencies. This relationship is exemplified in the electromagnetic spectrum, where high-energy gamma rays possess extremely short wavelengths and high frequencies, while low-energy radio waves have long wavelengths and low frequencies.
Frequency measures the number of oscillations or cycles per second. Higher frequency corresponds to higher energy and shorter wavelength. For example, visible light with a shorter wavelength, such as blue light, has a higher frequency and therefore carries more energy than red light with a longer wavelength.
Understanding this inverse relationship is crucial in various fields. In optics, it helps explain the dispersion of light through prisms. In particle physics, it underpins the behavior of photons and the particle-wave duality of light.
In conclusion, the inverse relationship between energy, frequency, and wavelength is a fundamental principle in physics. As we navigate the electromagnetic spectrum, from low-energy radio waves to high-energy gamma rays, this relationship guides our understanding of the behavior of light and other forms of electromagnetic radiation.
Energy Proportional to Frequency: Unveiling the Importance of Planck’s Constant
- Introduce Planck’s constant (h) and its role in relating energy to frequency.
- Explain the formula E = hν, where E represents energy, h is Planck’s constant, and ν is frequency.
Energy Proportional to Frequency: Unveiling the Importance of Planck’s Constant
In the realm of physics, energy and frequency are two fundamental properties that are inextricably linked. The elusive connection between them is unveiled through the brilliance of Planck’s constant, a pivotal player in the quantum world.
Imagine a vibrant ocean of electromagnetic radiation, encompassing a vast expanse of wavelengths and frequencies. Each wave, whether it be a gentle radio wave or an energetic gamma ray, carries within it a unique energy. This energy, it turns out, is directly proportional to the wave’s frequency.
Enter Planck’s constant (h), a fundamental constant of nature. This enigmatic value acts as a bridge between energy and frequency, allowing us to quantify the relationship between them. In the equation E = hν, where E represents energy, h is Planck’s constant, and ν is frequency, we find the key to understanding this proportionality.
As the frequency of a wave increases, its energy also increases. This means that higher-frequency waves, such as X-rays and gamma rays, possess significantly more energy than lower-frequency waves like radio waves. Conversely, when the frequency of a wave decreases, its energy also decreases.
Planck’s constant serves as a universal conversion factor, enabling scientists to calculate the energy of a wave given its frequency and vice versa. This profound relationship has wide-ranging implications, shaping our understanding of everything from the behavior of light to the properties of subatomic particles.
Shorter Wavelength, Higher Frequency: Unveiling the Link between Oscillations and Energy
In the realm of electromagnetic waves, the dance of wavelength, frequency, and energy unfolds an enchanting spectacle. Wavelength represents the distance between two consecutive peaks or troughs in an electromagnetic wave, while frequency measures the number of oscillations or cycles per second. Together, they orchestrate a symphony of energy, where shorter wavelengths waltz hand-in-hand with higher frequencies, giving rise to an energetic crescendo.
Imagine a captivating melody played on a violin’s strings. As the violinist presses down on a string, it vibrates faster, increasing the frequency of the sound waves it produces. Simultaneously, the wavelength of these waves becomes shorter, as the string’s oscillations become more frequent. This mesmerizing interplay is further illuminated by the formula E = hν, where E represents energy, h is Planck’s constant, and ν is frequency. The equation reveals that higher frequencies correspond to higher energy levels.
In the grand symphony of electromagnetic radiation, the relationship between wavelength, frequency, and energy manifests itself in a myriad of forms. From the gentle whispers of radio waves, with their long wavelengths and low frequencies, to the piercing cries of gamma rays, possessing short wavelengths and high frequencies, the electromagnetic spectrum paints a vibrant canvas of energy.
This enigmatic dance between wavelength, frequency, and energy holds profound implications across diverse scientific disciplines. In quantum physics, Planck’s constant plays a pivotal role, linking the energy of photons, quanta of light, to their frequency. Moreover, in fields ranging from optics to medicine, the manipulation of wavelength and frequency has led to groundbreaking advancements, such as lasers and diagnostic imaging techniques.
So, as we delve deeper into the enigmatic world of electromagnetic waves, let us embrace the melody of wavelength, frequency, and energy, a symphony that reveals the very fabric of our universe.
Shorter Wavelength, Higher Energy: Exploring the Interplay of Wavelength and Energy
- Reinforce the concept that shorter wavelengths indicate higher energy.
- Emphasize that higher energy corresponds to higher frequency and shorter wavelength.
Shorter Wavelength, Higher Energy: Exploring the Interplay of Wavelength and Energy
The fascinating world of electromagnetic waves unveils a captivating relationship between their wavelength and energy, with shorter wavelengths corresponding to higher energy. This interplay holds profound implications across the cosmos, from the vibrant colors we perceive to the very nature of light itself.
Imagine a mesmerizing light spectrum, where each color pulsates with a unique energy. As we traverse from the deep reds towards the vibrant violets, the wavelength – the distance between consecutive peaks or troughs of the electromagnetic waves – steadily decreases. This decrease in wavelength signifies an increase in energy.
This inverse relationship is elegantly captured by Planck’s constant, a fundamental constant in quantum physics. Planck’s constant relates the energy (E) of a photon, the fundamental particle of light, to its frequency (ν), a measure of its oscillations per second, as E = hν. As the frequency increases, the wavelength decreases, resulting in a corresponding increase in energy.
This harmonious dance between wavelength and energy manifests itself in countless phenomena. The shorter wavelengths of ultraviolet and X-rays, for instance, possess the energy to penetrate materials and even damage cellular structures, while the longer wavelengths of radio waves gently envelop our surroundings, carrying information across vast distances.
The electromagnetic spectrum serves as a testament to this wavelength-energy interplay. Spanning from the low-energy, long-wavelength radio waves to the high-energy, short-wavelength gamma rays, it encompasses a vast range of energies, each corresponding to a specific wavelength.
Understanding this inverse relationship empowers us to harness the energy of light for various applications. From solar cells that convert sunlight into electricity to lasers that emit highly focused beams, the manipulation of wavelength and energy has revolutionized our technological landscape.
In essence, the shorter the wavelength, the higher the energy. This interplay forms the cornerstone of our perception of light and underpins countless phenomena in the universe, from the colors we experience to the very fabric of our digital world. By embracing this captivating relationship, we unravel the secrets of light and unlock its boundless potential.
Longer Wavelength, Lower Frequency: Unraveling the Inverse Relationship
- Explain that longer wavelengths correspond to lower frequencies.
- Describe how lower frequencies result in decreased energy according to the formula E = hν.
Longer Wavelength, Lower Frequency: Unveiling the Inverse Relationship
The world of electromagnetic radiation is a fascinating realm where wavelengths and frequencies dance in an intricate waltz, each dictating the other’s characteristics. In this symphony of waves, a fundamental relationship exists: as wavelengths grow longer, their frequencies diminish. This inverse correlation reveals the intimate connection between the energy carried by these waves and their oscillations.
Decreasing Energy with Lower Frequencies
The energy of an electromagnetic wave is directly proportional to its frequency. This means that as the frequency decreases, so does the energy. This relationship is elegantly captured by the famous Planck’s equation, which states that energy (E) is equal to Planck’s constant (h) multiplied by frequency (ν): E = hν.
As wavelengths increase, frequencies decrease, leading to a concomitant decrease in energy. This phenomenon is evident throughout the electromagnetic spectrum, from the long, low-energy radio waves to the short, high-energy gamma rays.
Understanding the Inverse Relationship
Imagine a pendulum swinging. As the pendulum swings, it creates a wave that travels through space. The wavelength of this wave is the distance between two consecutive peaks or troughs, while the frequency is the number of times the pendulum swings per second.
Now, consider two pendulums: one with a long wavelength (swinging slowly) and one with a short wavelength (swinging quickly). The pendulum with the longer wavelength will have a lower frequency and, consequently, less energy. Conversely, the pendulum with the shorter wavelength will have a higher frequency and more energy.
The inverse relationship between wavelength and frequency is a fundamental aspect of electromagnetic radiation, revealing the interconnectedness of these two properties. As wavelengths lengthen, frequencies dwindle, resulting in a decrease in energy. This relationship underscores the interplay between these waves and their ability to interact with matter and the world around us.
Understanding the Inverse Relationship Between Wavelength and Energy
In the world of electromagnetic radiation, the trio of wavelength, energy, and frequency dance in an intricate balance. Just as the ebb and flow of the waves in the ocean shape the shoreline, these fundamental properties sculpt the spectrum of electromagnetic radiation.
Longer Wavelengths, Lower Energy
Among this fascinating trio, wavelength stands as the distance between consecutive peaks or troughs in an electromagnetic wave. Its inverse relationship with energy means that as wavelengths grow longer, the energy carried by the wave diminishes.
This phenomenon can be understood by envisioning an ocean wave. A long, gentle swell gently laps against the shore, carrying less energy than a short, powerful wave that crashes dramatically upon the sand. In the same way, longer wavelengths in the electromagnetic spectrum, such as radio waves and infrared radiation, possess lower energy levels compared to their shorter-wavelength counterparts.
The Spectrum of Electromagnetic Radiation
The electromagnetic spectrum, an orchestra of wavelengths, encompasses the entire range of electromagnetic waves. At one end of this spectrum reside radio waves, characterized by their exceptionally long wavelengths and low energy. On the opposite end, gamma rays shine with their extremely short wavelengths and high energy levels.
Within this vast spectrum, numerous other types of radiation exist, each with its unique wavelength and energy attributes. Microwave ovens utilize microwaves, while ultraviolet rays are found in sunlight. X-rays, used in medical imaging, lie in the intermediate energy range.
Applications in the Real World
The inverse relationship between wavelength and energy finds practical applications in various technologies. For instance, radio waves with their long wavelengths can penetrate buildings and other obstacles, making them ideal for communication and wireless devices. In contrast, microwaves are shorter in wavelength and thus reflect off objects more readily, a property utilized in radar systems.
The intricate relationship between wavelength, energy, and frequency underscores the fundamental nature of our universe. As we explore the electromagnetic spectrum, we delve deeper into the mysteries of energy, waves, and the boundless wonders that await us.
The Enchanting World of the Electromagnetic Spectrum: Unveiling the Dance of Wavelengths, Frequencies, and Energies
Imagine a vast tapestry woven with an infinite array of colors, from the vibrant hues of visible light to the elusive whispers of gamma rays. This magnificent canvas is known as the electromagnetic spectrum, a symphony of electromagnetic waves that permeate our universe. Each wave within this spectrum dances with a distinct rhythm, characterized by its wavelength, frequency, and energy.
The Inverse Tango: Wavelength, Frequency, and Energy
At the heart of this ethereal realm lies an elegant waltz, an inverse relationship between wavelength, frequency, and energy. As the wavelength of a wave increases, its frequency and energy gracefully diminish. Conversely, when the wavelength shortens, frequency and energy soar.
Planck’s Constant: The Quantum Transformer
In this mesmerizing dance, Planck’s constant (h) plays the role of a maestro, orchestrating the harmonious conversion of frequency to energy. The energy of an electromagnetic wave, denoted by E, is directly proportional to its frequency, ν:
E = hν
The Enigma of Shorter Wavelengths and Higher Energies
As we journey through the electromagnetic spectrum from longer to shorter wavelengths, we encounter an intriguing paradox. Shorter wavelengths possess a higher frequency and, thus, carry more energy. This harmonious interplay of wavelength, frequency, and energy governs the very nature of our universe.
The Electromagnetic Spectrum: A Cosmic Symphony
The electromagnetic spectrum unfolds before us like a cosmic symphony, with each region resonating with a unique set of properties:
- Radio waves: Immense wavelengths and low frequencies, used in communication and remote sensing.
- Microwaves: Shorter wavelengths and higher frequencies, employed in cooking and telecommunication.
- Infrared radiation: Even shorter wavelengths, responsible for heat transfer and night vision.
- Visible light: The vibrant hues we perceive, ranging from red (longest wavelength) to violet (shortest wavelength).
- Ultraviolet radiation: Invisible to the human eye, with wavelengths shorter than visible light, used in sterilization and tanning.
- X-rays: Highly energetic, penetrating radiation, crucial in medical imaging.
- Gamma rays: The most energetic electromagnetic waves, originating from nuclear reactions and cosmic events.
Frequency, Wavelength, Energy: Unveiling the Cosmic Code
Frequency, wavelength, and energy are the interwoven threads that paint the tapestry of the electromagnetic spectrum. Frequency measures the number of oscillations per second, wavelength determines the distance between wave crests, and energy embodies the power to perform work. Together, these fundamental concepts unlock the mysteries of light, heat, and the very fabric of our universe.
Planck’s Constant: The Catalyst of the Quantum Realm
Introduction:
Unlocking the enigmatic world of quantum physics, we encounter Planck’s constant (h), a fundamental entity that governs the interplay between energy and electromagnetic radiation. It is the key that unravels the intricate dance of photons, the quintessential particles of light, and their energy.
Planck’s Saga: A Revolutionary Revelation
In the annals of science, Max Planck’s quest to decipher the enigma of blackbody radiation led to a paradigm shift. His audacious hypothesis, that the energy of a photon is quantized, was a revolutionary stroke. This quantization, elegantly encapsulated in the formula E = hν, asserted that the energy (E) of a photon is directly proportional to its frequency (ν), meticulously bridged by Planck’s constant (h).
Quantum Threshold: The Birth of h
h, a constant with a minuscule value of 6.62607015 × 10^-34 joule-seconds, emerged as the cornerstone of quantum physics. It established that energy exists in discrete packets, or quanta, challenging the classical notion of continuous energy. This discretization marked a profound departure from the classical paradigm and paved the way for a new understanding of the quantum realm.
Photons in Motion: Frequency and Energy
Planck’s revelation illuminated the deep connection between frequency (ν) and energy (E) for photons. Higher frequencies correspond to more energetic photons, while lower frequencies carry less energy. This relationship underscores the quantum nature of light, where each photon embodies a quantized unit of energy.
Conclusion:
Planck’s constant (h) is a cornerstone of quantum physics, a fundamental constant that illuminates the quantized nature of energy. It unveils the profound connection between the energy and frequency of photons, establishing the quantum realm as a realm of discrete energy packets. Planck’s legacy continues to inspire scientific exploration, guiding our understanding of the intricate tapestry of the universe at its most fundamental level.
Frequency (ν): Unveiling the Rhythm of Energy
In the world of electromagnetic radiation, frequency reigns supreme as the measure of how often an electromagnetic wave oscillates or completes a cycle per second. This intrinsic property, denoted by the symbol ν, plays a pivotal role in determining the energy and wavelength of the radiation.
Imagine a swinging pendulum, its rhythmic sway exemplifying the concept of frequency. The faster the pendulum swings, the higher its frequency, and the shorter the time it takes to complete each oscillation. Similarly, in the realm of electromagnetic waves, higher frequencies correspond to faster oscillations and shorter wavelengths.
This inverse relationship between frequency and wavelength is a fundamental characteristic of electromagnetic radiation. As frequency increases, wavelength decreases, and vice versa. This interplay is captured by the formula:
c = λν
where c represents the speed of light, λ represents wavelength, and ν represents frequency. As the speed of light is a constant, any increase in frequency must be accompanied by a decrease in wavelength, and conversely, a decrease in frequency entails an increase in wavelength.
The significance of frequency extends beyond its role in determining wavelength. It also holds a profound relationship with energy. Albert Einstein’s groundbreaking equation, E = hν, unveiled this fundamental connection. Here, E represents energy, h is Planck’s constant, and ν is frequency. This equation highlights the direct proportionality between energy and frequency. Higher frequencies correspond to higher energy, while lower frequencies correspond to lower energy.
In essence, frequency serves as a key to understanding the energetic nature of electromagnetic radiation. It dictates the rhythm of oscillations, determines wavelength, and ultimately governs the amount of energy carried by the wave. From the gentle hum of radio waves to the penetrating power of gamma rays, frequency orchestrates the symphony of electromagnetic radiation.
Wavelength (λ): Unraveling the Distance Between Peaks
Wavelength (λ), a fundamental property of electromagnetic waves, quantifies the distance between two consecutive peaks or troughs. It plays a pivotal role in understanding the intricate relationship between energy, frequency, and the nature of light.
Shorter Wavelengths, Higher Energy
The inverse relationship between wavelength and energy dictates that shorter wavelengths correspond to higher energy. This phenomenon is evident across the electromagnetic spectrum, from high-energy gamma rays to low-energy radio waves. As the wavelength decreases, the energy content of the waves increases.
Consequence of Shorter Wavelengths
The increased energy of shorter wavelengths has profound consequences. For instance, ultraviolet (UV) radiation, with its shorter wavelengths, possesses higher energy than visible light, enabling it to interact with matter in ways visible light cannot. This interaction can lead to chemical reactions, such as those responsible for suntans or DNA damage.
Wavelength, a defining characteristic of electromagnetic waves, reveals the inverse relationship between energy and frequency. Shorter wavelengths, accompanied by higher energy, underscore the dynamic nature of light and its interactions with the physical world, shaping the very fabric of our universe.
Energy (E): The Power to Perform Work
- Define energy (E) as the capacity to do work or produce heat.
- Describe how energy is related to frequency and wavelength through Planck’s constant, with higher energy corresponding to higher frequency and shorter wavelength.
Energy (E): The Power to Perform Work
In the realm of physics, energy (E) reigns supreme as the fundamental capacity to do work or produce heat. It’s the driving force behind every movement, transformation, and interaction in the universe.
Energy manifests itself in myriad forms, from the mechanical energy of a moving car to the thermal energy of a warm coffee. However, one of the most captivating and enigmatic forms of energy is electromagnetic radiation, the very stuff that makes up light, radio waves, and X-rays.
Electromagnetic radiation possesses three fundamental characteristics: frequency (ν), wavelength (λ), and energy (E). These three properties are intricately intertwined, dancing in a delicate balance that reveals the secrets of the quantum world.
The frequency (ν) of electromagnetic radiation measures the number of oscillations or cycles it undergoes per second. A high frequency corresponds to a shorter time interval between oscillations, while a low frequency indicates a longer time interval.
Wavelength (λ), on the other hand, quantifies the distance between two consecutive peaks or troughs in the electromagnetic wave. A short wavelength signifies a smaller distance between peaks, while a long wavelength represents a larger distance.
Now, here comes the magic: the connection between energy, frequency, and wavelength. According to Planck’s constant (h), the energy (E) of a photon – the fundamental unit of electromagnetic radiation – is directly proportional to its frequency (ν) and inversely proportional to its wavelength (λ):
E = hν = hc/λ
This formula, etched into the annals of physics, reveals that shorter wavelengths correspond to higher energy and vice versa. Conversely, higher frequencies correspond to higher energy and vice versa, forming an inseparable trinity.
In practical terms, this relationship explains why X-rays, with their extremely short wavelengths, possess such potent energy, capable of penetrating dense materials. Radio waves, on the other hand, with their long wavelengths, carry a considerably lower energy.
Understanding the interplay between energy, frequency, and wavelength is not only essential for physicists but also for anyone seeking to unravel the mysteries of electromagnetism, optics, and the quantum world. It unlocks the door to a realm of phenomena, from the behavior of light to the functioning of lasers, where energy, frequency, and wavelength dance in perfect harmony.