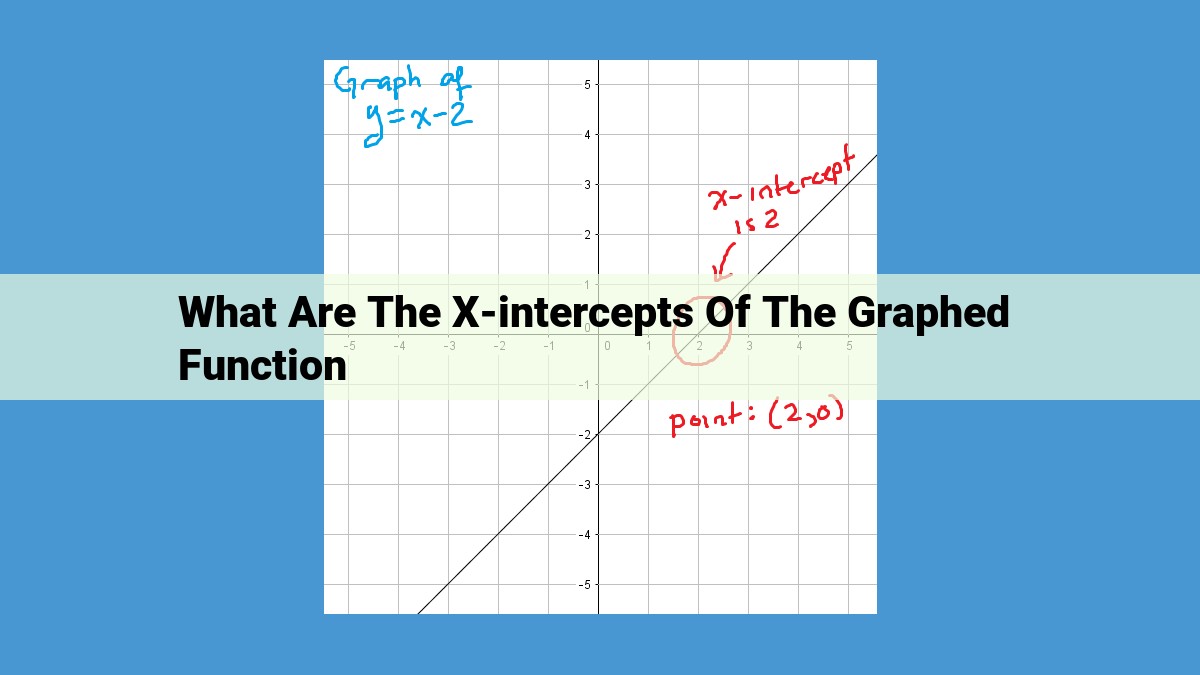
X-intercepts are points on a graph where a function’s value equals zero. They are also known as roots or zeros. To find X-intercepts, set the function’s equation to zero and solve for x. Additionally, factors can help find X-intercepts using the factor theorem, which states that if a polynomial f(x) has a factor of (x – a), then a is a root of f(x). By finding the roots of a polynomial using its factors, the corresponding X-intercepts can be determined.
What are X-Intercepts?
- Definition of X-intercepts as points where a function’s value is zero
- Synonyms for X-intercepts: roots and zeros
What Are X-Intercepts?
When a function’s value is zero, it intersects the x-axis. These points of intersection are called X-intercepts. They are also known as roots and zeros.
Understanding Roots and Zeros
- Roots: The x-coordinates of X-intercepts. They represent the values of x that make the function equal to zero.
- Zeros: Another term for X-intercepts. They indicate the points where the function crosses the x-axis.
Finding X-Intercepts
To find X-intercepts, we set the function’s equation equal to zero and solve for x. This gives us the values of x where the function intersects the x-axis.
The Role of Factors
A polynomial is an expression with constants and variables raised to positive integer powers. Factors are expressions that form a polynomial. The factor theorem states that if (x – a) is a factor of f(x), then a is a root of f(x).
Using Factors to Find X-Intercepts
We can use the factor theorem to find the roots of a polynomial:
- Find all the factors of (x – a).
- Set each factor equal to zero and solve for x.
- These values of x are the roots of the polynomial.
- The roots correspond to the X-intercepts of the function represented by the polynomial.
Roots and Zeros: Unveiling the Secrets of X-Intercepts
In the enigmatic world of algebra, X-intercepts stand as pivotal points where functions dance with the x-axis, their values momentarily reduced to zero. These elusive coordinates, also known as roots and zeros, hold the key to unlocking the behavior of polynomials and other functions.
Like buried treasures hidden beneath layers of mathematical complexity, roots reveal the x-values at which functions cross the x-axis. These critical points partition the graph into distinct regions, each with its own unique characteristics. For instance, the roots of a quadratic equation determine whether its parabola opens upward or downward.
Another moniker for X-intercepts, zeros, aptly captures their essence as points where functions vanish into nothingness. They represent the values of the independent variable for which the dependent variable evaluates to 0. These zeros serve as vital reference points, offering insights into the function’s behavior at specific inputs.
By unraveling the mysteries of roots and zeros, mathematicians and scientists gain invaluable knowledge about the functions they study. These enigmatic coordinates provide a glimpse into the hidden workings of polynomial equations, enabling us to predict their behavior and harness their power.
Finding X-Intercepts: Unveiling the Secrets of Zero Points
In the world of algebra, a graph’s x-intercepts play a pivotal role in understanding its behavior. These points, where the graph meets the x-axis, signify where the function’s value is equal to zero. Finding these intersections is crucial for analyzing the function’s characteristics and solving equations.
The process of finding x-intercepts begins with setting the function’s equation equal to zero. This ensures that we’re isolating the values of x that make the function equal to zero. For example, if the function is f(x) = x² – 4, we would set f(x) = 0 and solve for x.
Solving for x involves manipulating the equation to isolate the variable. In our example, we would start by adding 4 to both sides of the equation, which gives us x² = 4. Finally, we would take the square root of both sides, resulting in x = ±2.
These values of x, -2 and 2, represent the x-intercepts of the function f(x) = x² – 4. They indicate that the graph crosses the x-axis at (-2, 0) and (2, 0). By finding these intersections, we gain valuable insights into the function’s behavior and can determine where it equals zero.
Factors: The Building Blocks of Polynomials
In the realm of mathematics, polynomials stand as expressions that combine constants and variables, each raised to positive integer powers. These polynomials can be broken down into their fundamental components, known as factors.
Think of a polynomial as a skyscraper, towering over a city. Just as the skyscraper is composed of countless bricks, so too is a polynomial made up of factors. Each brick represents a variable or a constant, and their arrangement within the polynomial determines its overall form.
For instance, consider the polynomial x² – 4. This polynomial is a sum of two smaller factors: (x + 2) and (x – 2). These factors, like the bricks of a skyscraper, collectively define the behavior of the polynomial as a whole.
Unveiling the Secrets of the Factor Theorem: A Journey to Find X-Intercepts
In the realm of mathematics, the Factor Theorem stands as a powerful tool for unraveling the mysteries of polynomial functions and revealing their hidden roots. Join us as we embark on a storytelling adventure to unlock the secrets of the Factor Theorem and discover its invaluable role in finding X-intercepts.
The Factor Theorem: A Guiding Light
Imagine a polynomial function, a complex expression involving constants and variables adorned with positive integer exponents. The Factor Theorem emerges as a beacon of clarity, illuminating a fundamental connection between factors and roots. It proclaims that if a polynomial function, let’s call it f(x), possesses a factor of (x – a), then the tantalizing value of a holds the key to uncovering a root of f(x). This profound insight sets the stage for our quest to locate those elusive X-intercepts.
The Path to X-Intercept Glory
Armed with the newfound knowledge of the Factor Theorem, our journey continues. We venture into the realm of polynomials, dissecting them into their constituent factors. By skillfully factoring a polynomial, we unlock valuable clues that lead us to the roots we seek. Remember, the roots of a polynomial function are the x-coordinates of its X-intercepts.
A Guiding Example
To illustrate the power of the Factor Theorem, let’s unveil the secrets of a particular polynomial, f(x) = x^2 – 5x + 6. Factoring this expression yields two factors: (x – 2) and (x – 3). Eureka! According to the Factor Theorem, both 2 and 3 are roots of f(x), revealing the X-intercepts at (2, 0) and (3, 0).
Embark on Your Own Factor Theorem Adventure
Emboldened by our newfound knowledge, let us now embark on our own Factor Theorem adventures. Choose a polynomial function, wield the tools of factoring, and unravel its secrets. By identifying the factors of your function, you will uncover its roots and illuminate the X-intercepts that lie in wait.
May the Factor Theorem be your guiding star as you navigate the intricate world of polynomial functions. Remember, with each factor you discover, you are one step closer to unmasking the X-intercepts and illuminating the mysteries that lie within.
Using Factors to Find X-Intercepts: A Step-by-Step Guide
In the realm of mathematics, understanding the concept of X-intercepts is crucial. They represent the points where a function’s value is zero, offering valuable insights into a function’s behavior. To unravel the mystery of finding X-intercepts, we turn to the power of factors.
The Factor Theorem: A Key to Unlocking X-Intercepts
The factor theorem provides us with a powerful tool to find the roots of a polynomial, which are essentially the x-coordinates of X-intercepts. This theorem states that if a polynomial f(x) has a factor of (x – a), then a is a root of f(x). In other words, if we can factor a polynomial into linear factors, we can effortlessly identify its X-intercepts.
Step-by-Step Demonstration: Uncovering X-Intercepts
Let’s say we have the polynomial f(x) = x³ – 2x² – 5x + 6. To find its X-intercepts, we follow these steps:
-
Factor the polynomial: Using polynomial factoring techniques, we can factor f(x) as f(x) = (x – 2)(x² + x – 3).
-
Identify the roots: Using the factor theorem, we see that the factors of f(x) are (x – 2) and (x² + x – 3). Therefore, the roots of the polynomial are x = 2 and the roots of the quadratic factor x = -3 and x = 1.
-
Locate the X-intercepts: The roots of the polynomial correspond to the x-coordinates of the X-intercepts. Thus, the X-intercepts are (-3, 0), (1, 0), and (2, 0).
By utilizing the factor theorem and factoring techniques, we have effectively determined the X-intercepts of the polynomial f(x). This approach provides a systematic and efficient method to uncover these important points that reveal crucial information about a function’s behavior.